Produced by Charles Wells Revised 2017-02-22 Introduction to this website website TOC website index blog head of chapter on Numbers
A real number is a number that can be represented as a (possibly infinite) decimal expansion, such as $2.56$, $-3$ (which is $-3.0$), $1/3$ (which has the infinite decimal expansion $0.333...$), and $\pi$. Every integer and every rational number is a real number, but numbers such as $\sqrt{2}$ and $\pi$ are real numbers that are not rational.
The real numbers are closed under addition, subtraction, and multiplication, as well as division by a nonzero number.
Notice that these are exactly the same arithmetic closure properties that rational numbers have. In the previous sections in this chapter on numbers, each new number system -- natural numbers, integers and rational numbers -- were closed under more arithmetic operations than the earlier ones. We don't appear to have gained anything concerning arithmetic operations in going from the rationals to the reals.
The real numbers do allow you to find zeroes of some polynomials that don't have rational zeroes. For example, the equation $x^2-2=0$ has the root $x=\sqrt{2}$, which is a real number but not a rational number. However, you get only some zeroes of polynomials by going to the reals -- consider the equation $x^2+2=0$, which requires going to the complex numbers to get a root.
The real numbers are closed under another operation (not an algebraic operation) that rational numbers are not closed under:
The real numbers are closed under taking limits.
That fact is the primary reason real numbers are so important
in math, science and engineering.
Consider: The concepts of continuous function, derivative and integral -- the basic ideas in calculus and differential equations -- are all defined in terms of limits. Those are the basic building blocks of mathematical analysis, which provides most of the mathematical tools used by scientists and engineers.
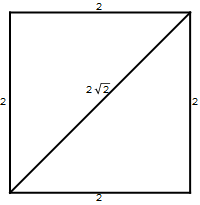
The length of any line segment is given by a positive real number.
 |
The diagonal of the square above has length $2\sqrt{2}$.
Measuring directed line segments requires the use of negative real numbers as well as positive ones. You can regard the diagonal above as a directed line segment. If you regard “left to right” as the positive direction (which is what we usually do), then if you measure it from right to left you get $-2\sqrt{2}$.
Real numbers are used to measure continuous variable quantities.
If you have $1.334 \text{ cm}^3$ of water in a jar you can add any additional small amount into it or you can withdraw any small amount from it. The volume does not suddenly jump from $1.334$ to $1.335$ – as you put in the water it goes up gradually from $1.334$ to $1.335$.
This explanation of “continuous quantity” is done in terms of how we think about continuous quantities, not in terms of a mathematical definition. In fact. since you can’t measure an amount smaller than one molecule of water, the volume does jump up in tiny discrete amounts. Because of quantum phenomena, temperature and speed change in tiny jumps, too (much tinier than molecules).
Quantum jumps and individual molecules are ignored in large-scale physical applications because the scale at which they occur is so tiny it doesn’t matter. For such applications, physicists and chemists (and cooks and traffic policemen!) think of the quantities they are measuring as continuous, even though at tiny scales they are not.
The fact that scientists and engineers treat changes of physical quantities as continuous, ignoring the fact that they are not continuous at tiny scales, is sometimes called the "continuum hypothesis". This is not what mathematicians mean by that phrase: see continuum hypothesis in Wikipedia.
It is useful to visualize the set of real numbers as the real line (or the number line).
The real line goes off to infinity in both directions. Each real number represents a location on the real line. Some locations are shown here:
 |
The locations are commonly called points on the real line. This can lead to a seriously mistaken mental image of the reals as a row of points, like beads. Just as in the case of the rationals, there is no real number “just to the right” of a given real number.
In this section, I will go into more detail about the decimal representation of the real numbers. There are two reasons for doing this.
See also The Number Line and Why the Number Line Freaks Me Out.
The decimal representation of a real number is also called its decimal expansion. A representation can be given to other bases besides $10$; more about that here.
The decimal representation of a real number gives the approximate location of the number on the real line as its directed distance from $0$.
It is customary to put a bar over a sequence of digits at the end of a decimal representation to indicate that the sequence is repeated forever.
If you give the first few decimal places of a real number, you are giving an approximation to it. Mathematicians on the one hand and scientists and engineers on the other tend to treat expressions such as $3.14159$ in two different ways:
Computer languages typically treat integers as if they were distinct from real numbers. In particular, many languages have the convention that the expression ‘$2$’ denotes the integer and the expression ‘$2.0$’ denotes the real number. Mathematicians do not use this convention. They usually regard the integer $2$ and the real number $2.0$ as the same mathematical object.
The decimal representation of a real number is shorthand for a particular infinite series.
Suppose the part before the decimal place of a real number $r$ is the integer $n$, and the part after the decimal place is\[{{d}_{1}}{{d}_{2}}{{d}_{3}}...\]where ${{d}_{i}}$ is the digit in the $i$th place. (For example, for $\pi$, $n=3$, ${{d}_{1}}=1,\,\,\,{{d}_{2}}=4,\,\,\,{{d}_{3}}=1,$ and so forth.) Then the decimal notation $n.{{d}_{1}}{{d}_{2}}{{d}_{3}}...$ represents the limit of the infinite series\[n+\sum\limits_{i=1}^{\infty }{\frac{{{d}_{i}}}{{{10}^{i}}}}\]
The number $42\frac{1}{3}$ is exactly equal to the sum of the infinite series, which is represented by the expression $42.\overline{3}$.
If you stop the series after a finite number of terms, then the number is approximately equal to the resulting sum. For example, $42\frac{1}{3}$ is approximately equal to\[42+\frac{3}{10}+\frac{3}{100}+\frac{3}{1000}\]which is the same as $42.333\overline{0}$.
This inequality gives an estimate of the accuracy of this approximation:\[42.333\lt42\frac{1}{3}\lt42.334\]
The expression $42.\overline{3}$ must be thought of as including all the $3$'s all at once rather than as gradually extending to the right over an infinite period of time.
In ordinary English, the “…” often indicates continuing through time, as in this example
“They climbed to the top of the ridge, and saw another, higher ridge in the distance, so they walked to that ridge and climbed it, only to see another one still further away…”
But the situation with decimal representations is different:
The decimal representation of $42\frac{1}{3}$ as $42.333\ldots$
must be thought of as a complete,
infinitely long sequence of decimal digits,
every one of which (after the decimal point) is a “$3$” right now.
In the same way, you need to think of the decimal expansion of $\sqrt{2}$ as having all its decimal digits in place at once. Of course, in this case you have to calculate them in order. And note that calculating them is only finding out what they are. The digits are already there!
The preceding description is about how a mathematican thinks about infinite decimal expansions. The thinking has some sort of physical representation in your head that allows you to think about to the hundred millionth decimal place of $\sqrt{2}$ or of $\pi$ even if you don’t know what it is. This does not mean that you have an infinite number of slots in your brain, one for each decimal place! Nor does it mean that the infinite number of decimal places actually exist “somewhere”. After all, you can think about unicorns and they don’t actually exist somewhere.
Both the following statements are true:
These two statements don’t contradict each other. All three numbers have exact definitions.
The decimal representations of two different real numbers must be different from each other. However, two different decimal representations can, in certain circumstances, represent the same real number. This happens when the decimal representation ends in an infinite sequence of $9$’s or an infinite sequence of $0$’s.
The Wikipedia article "$0.\overline{9}$" is an elaborate discussion of the fact that $0.\overline{9}=1$, a fact that many students find hard to believe.
The integers can be thought of as beads or points in a row going to infinity in both directions. The real numbers go to infinity in both directions, too, but:
You must not think of the real numbers as a row of points.
That is because: between any two distinct real numbers there is another one. Specifically: If $r$ and $s$ are any distinct real numbers, then $\frac{r+s}{2}$ is a real number between them. This number $\frac{r+s}{2}$ is the average of $r$ and $s$, so it makes sense that it is between them. (There is a formal proof of this in the Glossary.) For example, you can check that if $r=\frac{5}{12}$and $s=\frac{1}{2}$, then $\frac{r+s}{2}=\frac{11}{24}$. Note that $r=\frac{10}{24}$ and $s=\frac{12}{24}$.
Just as in the case of the rational numbers, between any two different real numbers there is an infinite number of real numbers between them.
This work is licensed under a Creative Commons Attribution-ShareAlike 2.5 License.