abstractmath.org 2.0
help with abstract math

Produced by Charles Wells     Revised 2016-07-23

Introduction to this website    website TOC    website index   blog

Back to head of sets chapter

SETS: METAPHORS AND IMAGES

This section describes certain common images and metaphors we have for sets – and their dangers.

A set is a mathematical object

Example

The set $A:=\{3,5,6,7,8\}$ is a mathematical object. 

• $A$ is one object. It is not five different numbers.
• Its defining property is that the numbers $3$, $5$, $6$, $7$ and $8$ are elements $A$ and nothing else is an element of $A$.
• $A$ is not the same thing as its elements.  It is true that the integer $5$, for example, has a special relationship to $A$, namely it is one of the elements of $A$, but the set $A$ is an object that is separate from its elements.

Example

The set $\mathrm{R}$ of all real numbers is a single math object with unimaginably many elements.  You may think it impossibly hard to think of all the real numbers at once. But $\mathrm{R}$ is just one math object.  You don’t have to think about all the real numbers at once to think about $\mathrm{R}$, any more than you have to think about all the molecules of water in the Pacific Ocean at once to think about the Pacific Ocean.

A set is one mathematical object:
not many, not a bunch, but one object.

A set is not its notation

When you visualize the set $\{3,5,6,7,8\}$, the image you have may be the notation “$\{3,5,6,7,8\}$”. It is not entirely bad to visualize the notation when you think of this set, but remember that the notation has an irrelevant feature, namely the order in which the elements are written.  The set $\{3,5,6,7,8\}$ is the same set as the one denoted by $\{3,6,7,5,8\}$, but the notation $\{3,5,6,7,8\}$ is not the same as the notation $\{3,6,7,5,8\}$. So it is wrong to think that the notation is the set.

Similarly, for real $x$, $\left\{ x|x\gt6 \right\}=\left\{ x|x\ge 6\text{ and }x\ne 6 \right\}$ even though the notation before the equals sign is different from the notationa after it.

The same set can be described by many different notations.

A set is a container

You can think of a set as a container that holds all its elements.   This metaphor is good in some ways and bad in others.

• Good: Just like a set, container is a single object, different from any of the things it contains.  In fact, it is different from the whole bunch of things it contains.
• Bad: Consider the sets $A=\{3,5,6,7,8\}$ and $B$ the set of all odd integers. Then $3\in A$ and $3\in B$ and in fact $3\in A\cap B$.  How can one thing be in three different containers?
• Bad: Using the sets $A$ and $B$ just defined, note that $6\in A$ and $A\in \left\{ A,B\mathrm{} \right\}$. ($\left\{ A,B\mathrm{} \right\}$ is the set whose only elements are the sets $A$ and $B$.) But $6\notin \left\{ A,B\mathrm{} \right\}$.  This behavior is not at all the way we usually think of containers:  If you have a dime in a coin purse and the coin purse is in your pocket, you would say that the dime is in your pocket.

Venn Diagrams

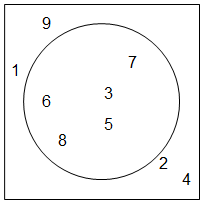
Venn Diagrams give a useful picture of relationships between a few sets portrayed as points inside a circle (or other closed curve). The circle is then a container and the elements of the set are shown as points inside the circle.

Example

The circle in the Venn diagram above represents the set $\{3,5,6,7,8\}$ shown as a subset of the integers between $1$ and $9$ inclusive. The element $3$ is shown as above $5$ and $7$ is northeast of $5$, and both those facts are completely irrelevant!

There is no good way to represent a finite set
that does not have irrelevant information
such as the location of the elements.

A set is a pointer

I prefer to think of the set $A=\{3,5,6,7,8\}$ as a mathematical object that has a special relationship with the numbers $3$, $5$, $6$, $7$ and $8$ that it does not have with any other objects. My mental image is a node called $A$ that has wires or arrows connecting that node to those five numbers and to nothing else. Those numbers can be moved around in the picture but that makes no difference – all that counts is the connections. (In that sense this picture is a directed graph.)

You may see a similarity between this and a pointer in a computer language. Typically a pointer in those languages will point to the head of a list and each entry in the list will point to another one. But the proper image for a set is that the pointer points to each one of them without preference – there is no ordering, implicit or otherwise. Another difference is that for sets, unlike computer language pointers, two different sets cannot point to exactly the same bunch of elements.

This work is licensed under a Creative Commons Attribution-ShareAlike 2.5 License.