
Produced by Charles Wells Revised 2017-02-06 Introduction to this website website TOC website index blog Back to top of Understanding Math chapter
Mathematics is the tinkertoy of metaphor.--Ellis D. Cooper
Half this game is 90% mental.–Yogi Berra
The language that nature speaks is mathematics. The language that ordinary human beings speak is metaphor. --Freeman Dyson
In this chapter, I say something about mental representations (metaphors and images) in general, and provide examples of how metaphors and images help us understand math – and how they can confuse us.
Pay special attention to the section called two levels! The distinction made there is vital but is often not made explicit.
Mental representations and other kinds of representations used in math are also discussed in in many other places, including other articles in abstractmath.org.
We think and talk about our experiences of the world in terms of images and metaphors that are ultimately derived from immediate physical experience. They are mental representations of our experiences.

We know what a pyramid looks like. But when we refer to the government’s food pyramid we are not talking about actual food piled up to make a pyramid. We are talking about a visual image of the pyramid.
We know by direct physical experience what it means to be warm or cold. We use these words as metaphors in many ways:
One basic fact about metaphors and images is that they apply only to certain aspects of the situation.
Our brains handle these aspects of mental representations easily and usually without our being conscious of them. They are one of the primary ways we understand the world.
It is not possible to imagine mathematics without its computational and formal aspects, but to focus exclusively on them destroys the subject.–William Byers
Mathematicians who work with a particular kind of mathematical object have mental representations of that type of object that help them understand it. These mental representations come in many forms. Most of them fit into one of the types below, but the list shouldn't be taken too seriously: Some representations fit more that of these types, and some may not fit into any of them except awkwardly.
Below I list some examples. Many of them refer to the arch function, the function defined by $h(t):=25-{{(t-5)}^{2}}$.






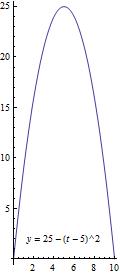
“Continuous functions don’t have gaps in the graph”. This is a visual image, and it is usually OK in calculus class.
But consider the curve defined by $y=25-(t-5)^2$ for every real $x$ except $x=1$. It is not defined at $x=1$ (and so the function is discontinuous there) but its graph looks exactly like the graph in the figure above because no matter how much you magnify it you can't see the gap.
So is there a gap or not?
This is a typical math example that teachers make up to raise your consciousness.
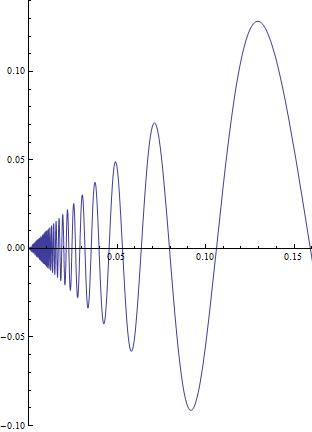
"Continuous functions can be drawn without lifting the chalk." This is true in most familiar cases (provided you draw the graph only on a finite interval). But consider the graph of the function defined by $f(0)=0$ and \[f(t)=t\sin\frac{1}{t}\ \ \ \ \ \ \ \ \ \ (0\lt t\lt 0.16)\] (see Split Definition). This curve is continuous and is infinitely long even though it is defined on a finite interval, so you can't draw it with a chalk at all, picking up the chalk or not. Note that it has no gaps.
I personally use visual images to remember relationships between abstract objects, as well. For example, if I think of three groups, two of which are isomorphic (for example $\mathbb{Z}/3$ and $\text{Alt}(3)$), I picture them as in three different places in my head with a connection between the two isomorphic ones.
Here I give some examples of thinking of math objects in terms of the notation used to name them. There is much more about notation as mathematical representation in these sections of abmath:
Notation is both something you visualize in your head and also a physical representation of the object. In fact notation can also be thought of as a mathematical object in itself: this point of view is worked out in detail in mathematical logic and in theoretical computing science. If you think about what notation “really is” a lot, you can easily get a headache…
You can think of the set containing $1$, $3$ and $5$ and nothing else as represented by its common list notation $\{1, 3, 5\}$. But remember that $\{5, 1,3\}$ is another notation for the same set. In other words the list notation has irrelevant features – the order in which the elements are listed in this case.

It is common to think of a function as a process: you put in a number (or other object) and the process produces another number or other object. There are examples in Images and metaphors for functions.
Let's divide $66$ by $7$ using long division. The process consists of writing down the decimal places one by one.
You can continue with the procedure to get as many decimal places as you wish of $\frac{66}{7}$.
The sequence of actions just listed is quite difficult to follow. What is difficult is not understanding what they say to do, but where did they get the numbers? So do this exercise!
Check that the procedure above is exactly what you do to divide $66$ by $7$ by the usual method taught in grammar school:
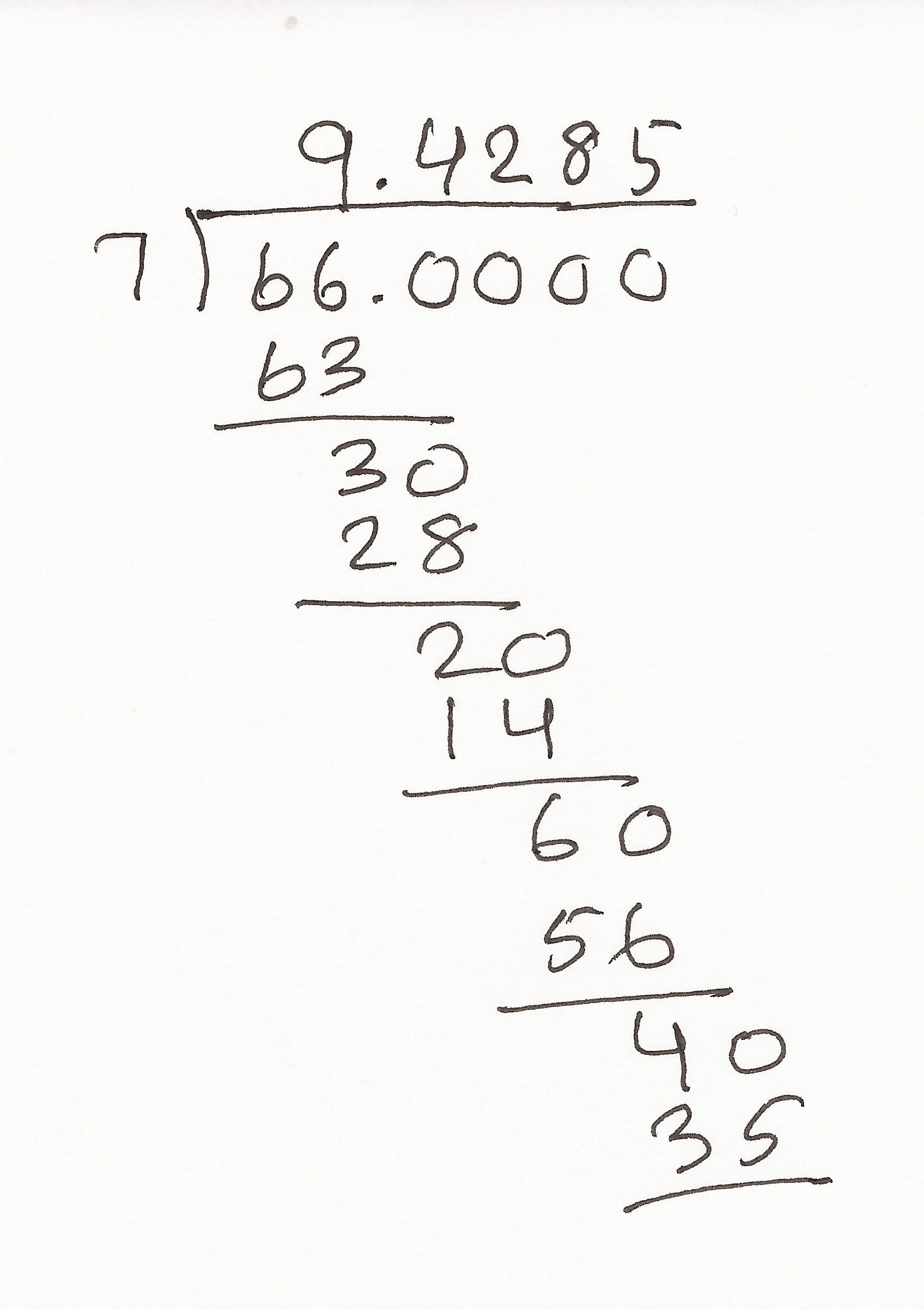
A particular kind of metaphor or image for a mathematical concept is that of a mathematical object that represents the concept.
Representations as math objects is discussed primarily in Representations and Models. The difference between representations as math objects and other kinds of mental representations (images and metaphors) is primarily that a math object has a precise mathematical definition. Even so, they are also mental representations.
Mental representations of a concept make up what is arguably the most important part of the mathematician's understanding of the concept.
Different mental representations of the same kind of object help you understand different aspects of the object.
|
Every important mathematical object |
But images and metaphors are also dangerous (see below).
We especially depend on metaphors and images to understand a math concept that is new to us . But if we work with it for awhile, finding lots of examples, and eventually proving theorems and providing counterexamples to conjectures, we begin to understand the concept in its own terms and the images and metaphors tend to fade away from our awareness.
Then, when someone asks us about this concept that we are now experts with, we trundle out our old images and metaphors – and are often surprised at how difficult and misleading our listener finds them!
Some mathematicians retreat from images and metaphors because of this and refuse to do more than state the definition and some theorems about the concept. They are wrong to do this. That behavior encourages the attitude of many people that
All three of these statements are half-truths.
There is no doubt that a lot of abstract math is hard to understand, but understanding is certainly made easier with the use of images and metaphors.
This website has many examples of useful mental representations. Usually, when a chapter discusses a particular type of mathematical object, say rational numbers, there will be a subhead entitled "Images and metaphors for rational numbers". This will suggest ways of thinking about them that many have found useful.
Images and metaphors have to be used at two different levels, depending on your purpose.
Math teachers and texts typically do not make an explicit distinction between these views, and you have to learn about it by osmosis. In practice, teachers and texts do make the distinction implicitly. They will say things like, “You can think about this theorem as …” and later saying, “Now we give a rigorous proof of the theorem.” Abstractmath.org makes this distinction explicit in many places throughout the site.
The kind of metaphors and images discussed in the mental representations section above make math rich, colorful and intriguing to think about. This is the rich view of math. The rich view is vitally important.
You expect the ball whose trajectory is modeled by the function h(t) above to slow down as it rises, so the derivative of h must be smaller at t = 4 than it is at t = 2. A mathematician might even say that that is an “informal proof” that $h'(4)<h'(2)$. A rigorous proof is given below.
When we are constructing a definition or proof, we cannot trust all those wonderful images and metaphors.
For the point of view of doing proofs, math objects must be thought of as inert (or static), like your pet rock. This means they
(See also abstract object).
Above, I gave an informal argument for this. The rigorous way to see that $h'(4)\lt h'(2)$ for the arch function is to calculate the derivative \[h'(t)=10-2t\] and plug in 4 and 2 to get \[h'(4)=10-8=2\] which is less than $h'(2)=10-4=6$.
Note the embedded phrases.
This argument picks out particular data about the function that prove the statement. It says nothing about anything slowing down as $t$ increases. It says nothing about anything at all changing.
The rigorous view does not apply to all abstract objects, but only to mathematical objects. See abstract objects for examples.
The price of metaphor is eternal vigilance.--Norbert Wiener
Every mental representation has flaws. Each one provides a way of thinking about an $A$ as a kind of $B$ in some respects. But the representation can have irrelevant features. People new to the subject will be tempted to think about $A$ as a kind of $B$ in inappropriate respects as well. This is a form of cognitive dissonance. The metaphors inherent in representations can also contradict each other. That is also a form of cognitive dissonance.
It may be that most difficulties students have with abstract math are based on not knowing which aspects of a given representation are applicable in a given situation. Indeed, on not being consciously aware that in general you must restrict the applicability of the mental pictures that come with a representation.
In abstractmath.org you will sometimes see this statement: “What is wrong with this metaphor:” (or image, or representation) to warn you about the flaws of that particular representation.
The graph of the arch function $h(t)$ makes it look like the two arms going downward become so nearly vertical that the curve has vertical asymptotes. But it does not have asymptotes. The function is defined at every point of the $x$-axis. For example, there is a point on the curve underneath the point $(999,0)$, namely $(999, -988011)$.
That graph is a picture that sits on your screen without moving. It gives a static picture of the set of points \[(t,25-{{(t-5)}^{2}})\] The function $h(t)$ can also be thought of as the path of a rocket, which is moving. So the two points of view contradict each other, which I think makes it hard for some students to "see" the movement when looking at the graph.
A set is sometimes described as a container. But consider: the integer 3 is "in" the set of all odd integers, and it is also "in" the set $\left\{ 1,\,2,\,3 \right\}$. How could something be in two containers at once? (More about this Images and Metaphors for Sets and in Some Specific Sets.)
Mathematicians think of the real numbers as constituting a line infinitely long in both directions, with each number as a point on the line. But this does not mean that you can think of the line as a row of points. See density of the real line.
We commonly think of functions as machines that turn one number into another. But this does not mean that, given any such function, we can construct a machine (or a program) that can calculate it. For many functions, it is not only impractical to do, it is theoretically impossible to do it. They are not computable. In other words, the machine picture of a function does not apply to all functions.
|
The images and
metaphors you use |
|
The
images and metaphors you use |
|
Only definitions and previously proved theorems |
It seems likely that cognitive phenomena such as images and metaphors are physically represented in the brain as collections of neurons connected in specific ways. Research on this topic is proceeding rapidly. Perhaps someday we will learn things about how we think physically that actually help us learn things about math.
In any case, thinking about mathematical objects as physically represented in your brain (not necessarily completely or correctly!) wipes out a lot of the dualistic talk about ideas and physical objects as separate kinds of things. Ideas, in particular math objects, are emergent constructs in the physical brain.
“Metaphor” is used in abstractmath.org to describe a type of thought configuration. It is an implicit conceptual identification of part of one type of situation with part of another.
Metaphors are a fundamental way we understand the world. In particular, they are a fundamental way we understand math.
The word “metaphor” is also used in rhetoric as the name of a type of figure of speech. Authors often refer to metaphor in the meaning of thought configuration as a conceptual metaphor. Other figures of speech, such as analogy, simile and synecdoche, correspond to conceptual metaphors as well. The quora article provides a useful explanation of the way "analogy", "simile" and "metaphor" ae used.
In the figure-of-speech literary usage of the word metaphor, "My love is like a red red rose" is a simile, not a metaphor; "My love is a red red rose" is a metaphor.
Michael Chorost, Your brain on metaphors. Chronicle of Higher Education, September 1, 2014.
Fauconnier, G. and Turner, M., The Way We Think: Conceptual Blending And The Mind's Hidden Complexities . Basic Books, 2008.
Lakoff, G., Women, Fire, and Dangerous Things. The University of Chicago Press, 1986.
Lakoff, G. and Mark Johnson, Metaphors We Live By. The University of Chicago Press, 1980.
Wikipedia, Conceptual metaphors.
Byers, W., How mathematicians Think. Princeton University Press, 2007.
Lakoff, G. and R. E. Núñez, Where mathematics Comes From. Basic Books, 2000.
Math Stack Exchange list of explanatory images in math.
Núñez, R. E., “Do Real Numbers Really Move?” Chapter in 18 Unconventional Essays on the Nature of mathematics, Reuben Hersh, Ed. Springer, 2006.
Vinner, S. and Tall, D. (1981). Concept image and concept definition in mathematics, with special reference to limits and continuity.
Charles Wells, Handbook of mathematical Discourse.
Images and metaphors for functions
Real numbers: images and metaphors
Representations of continuous functions
Representations of discrete functions
This work is licensed under a Creative Commons Attribution-ShareAlike 2.5 License.