abstractmath.org 2.0
help with abstract math

Produced by Charles Wells     Revised 2016-08-19

Introduction to this website    website TOC    website index   blog     Back to head of functions chapter

EXAMPLES OF FUNCTIONS

Basic functions

The examples given here:

• are basic types of functions that are used everywhere in abstract math
• are functions you need to be familiar with
• are (sigh) boring.

Identity function

For any set $A$, the identity function ${{\operatorname{id}}_{A}}:A\to A$ is the function that takes each element of $A$ to itself.

• This means that for any set $A$, for every element $a\in A$, ${{\operatorname{id}}_{A}}(a)=a$. For example, ${{\operatorname{id}}_{\mathbb{Z}}}(42)=42$.
• The identity function on a set $A$ can be thought of as the function that does nothing to each element of A.
• The identity function on $\mathbb{R}$ is the familiar function defined by $f(x)=x$.
• Another common notation for the identity function on $A$ is "${{1}_{A}}:A\to A$."
• The word "identity" has two other commonly used meanings.
• There is a different identity function for each different set. (See overloaded notation.)  These functions all have the “same” formula:  ${{\operatorname{id}}_{A}}(a)=a$ for every $a\in A$. But they are technically different functions because they have different domains.

Inclusion function

If $A\subseteq B$ (see inclusion), then the inclusion function $\operatorname{inc}:A\to B$ that takes every element in $A$ to the same element regarded as an element in $B$. In other words, $\operatorname{inc}(a)=a$ for every element $a\in A$.

• The inclusion map is often written $A\hookrightarrow B$.
• The graph of $\text{inc}$ is the same as the graph of ${{\operatorname{id}}_{A}}$ and they have the same domain, so that the only difference between them is what the codomain is.
• For any set $A$, $A\subseteq A$, so the identity function ${{\operatorname{id}}_{A}}:A\to A$ is an inclusion function.

Constant function

If $A$ and $B$ are nonempty sets and $b$ is a specific element of $B$, then then constant function ${{C}_{b}}:A\to B$ is the function that takes every element of $A$ to $b$; that is, ${{C}_{b}}(a)=b$ for all $a\in A$.

• The notation ${{C}_{b}}$ is not common.  There is no standard notation for constant functions.
• A constant function ${{C}_{b}}$ takes any element of $A$ to $b$.  It has a one-track mind.
• A constant function from $\mathbb{R}$ to $\mathbb{R}$ has a horizontal line as its graph.
• See the Wikipedia article Constant function.

Empty function

If $A$ is any set, there is exactly one function $E:\varnothing \to A$. This function is called the empty function.

• An identity function does nothing. An empty function has nothing to do.
• The graph of the empty function is the empty set, and so is its image.
• For any set $A$, there is exactly one empty function from $\varnothing\to A$.
• The empty function from $\varnothing\to A$ is an inclusion function vacuously.

Coordinate function

If $A$ and $B$ are sets, there are two coordinate functions ${{p}_{1}}:A\times B\to A$ and ${{p}_{2}}:A\times B\to B$, defined for $a\in A$ and $b\in B$ by ${{p}_{1}}(a,b)=a$ and ${{p}_{2}}(a,b)=b$.

• $A\times B$ is the set of all ordered pairs $(a,b)$ with $a\in A$ and $b\in B$. See cartesian product.
• Coordinate functions are also called projections.
• The coordinate function ${{p}_{i}}$ may be denoted by "${{\pi }_{i}}$".
• In general for an $n$-fold cartesian product, the function ${{p}_{i}}$ takes an $n$-tuple to its $i$th coordinate.
• If either $A$ or $B$ is empty, then so is $A\times B$.  In that case, each ${{p}_{i}}$ is the empty function.
• For any set $S$, there are two different coordinate functions ${{p}_{1}}:S\times S\to S$ and ${{p}_{2}}:S\times S\to S$.  For example, if $S$ is the set of real numbers, then ${{p}_{1}}(2,-3)=2$ and ${{p}_{2}}(2,-3)=-3$.

Sequences

A sequence is a list of math objects.

Example: A finite sequence

• The list $L:=(1,4,4,2,-3,-2)$ is a finite sequence of integers. The $3$rd entry in $L$ is $4$ and the $4$th entry is $2$.
• $L$ could be written as \[(n_1,n_2,n_3,n_4,n_5,n_6)\] and then one would say for example that $n_3=4$ and $n_4=2$.
• The index set of $L$ is the set ${1,2,3,4,5,6}$.
• A finite sequence is also called a tuple. $L$ is a 6-tuple. A $2$-tuple is the same thing as an ordered pair.

Example: An infinite sequence

• $S:=(1,4,9,16,25,\dots)$ (the $n$th entry is $n^2$) is an infinite sequence of integers.
• The index set of $S$ is the set of positive integers.
• Such a sequence may be written this way:\[S:=(n^2)\,,\,n>0\]

A basic fact about sequences

A sequence is a function on its index set.

This statement causes a major ratchet effect for some students. It looks like random nonsense until you suddenly understand it, after which it is totally obvious.

A sequence is a function. Its domain is the index set and the value at $i$ is the entry indexed as $i$ in the sequence.

Examples

• The sequence $L$ is the function $f:(1,2,3,4,5,6)\to\mathbb{Z}$ given by

  $f(1)=1$

  $f(2)=4$

  $f(3)=4$

  $f(4)=2$

  $f(5)=-3$

  $f(6)=-2$

• The infinite sequence $S$ is the function \[n\mapsto n^2:\mathbb{N}\to\mathbb{N}\] where $\mathbb{N}$ is the set of natural numbers (positive integers).

There is much more information on tuples and sequences in the Wikipedia articles Tuple and Sequence.

Binary operations

A binary operation on a set $S$ is a function $F:S\times S\to S$.  (See cartesian product).

• The operation of adding two real numbers gives a binary operation $(x,\,y)\mapsto x+y:\mathbb{R}\times \mathbb{R}\to \mathbb{R}$.
• Subtraction $-:\mathbb{R}\times \mathbb{R}\to \mathbb{R}$ is also a binary operation on the real numbers.  Observe that, unlike addition, it cannot be regarded as a binary operation on the positive real numbers. 
• Multiplication of real numbers is also a binary operation $(x,\,y)\mapsto xy:\mathbb{R}\times \mathbb{R}\to \mathbb{R}$.
• Division is not a binary operation on the real numbers because you can’t divide by $0$.  However, it is a binary operation $(x,\,y)\mapsto x/y:\mathbb{R}^*\times\mathbb{R}^*\to\mathbb{R}^*$ on the nonzero real numbers ("${\mathbb{R}^{*}}$" is standard notation for the set of all nonzero real numbers).
• Now look at the function $(x,\,y)\mapsto x/y:\mathbb{R}\times\mathbb{R}^*\to \mathbb{R}$. It is well defined since $0/y$ is defined even though $y/0$ is not. This is a perfectly good function but strictly speaking it is not a binary operation because by definition a binary operation has to fit the pattern $F:S\times S\to S$ where all three sets are the same.
• For any set $S$, the two projections ${{p}_{1}}:S\times S\to S$ and ${{p}_{2}}:S\times S\to S$ are both binary operations on $S$.
• The greatest common divisor function $\operatorname{GCD}:\mathbb{N}\times\mathbb{N}$ is a binary operation on the set of all nonnegative integers.
• With a binary operation symbol, infix notation is usually used: the name of the binary operation is put between the arguments.  For example we write $3 + 5 = 8$, not $+(3, 5) = 8$.  Note that there are no symbols for the $\text{GCD}$ function and for the projections from a cartesian product.
• Binary operations are the basis of most of algebra.

Consciousness-expanding examples of functions

In this section I give you examples of really weird functions that you may never have thought of as functions before, because if you are a beginner in abstract math, you probably need to:

Loosen up narrow-minded ideas about what a function is

Other consciousness-expanding examples of functions are listed in an appendix.

Example: "Split"

A function can be given by different rules on different parts of its domain. It is still one function.

Let $F:[0,1]\to\mathbb{R}$ be defined by \[F(x):=\left\{ \begin{align} 2x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(0\le x\le 0.5) \\ 3(x-1)^2\,\,\,\,(0.5\lt x\le 1) \\ \end{align}\right.\] This is the graph of $F$:

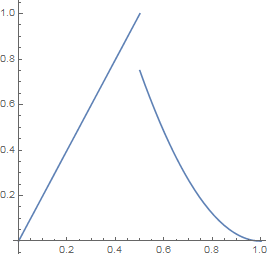
• $F$ is given by a split definition.  It is defined by one formula for part of its domain and by another on the rest. $F$ is nevertheless one function, defined on the closed interval $[0,1]$.
• $F$ is not continuous at $x=0.5$.
• $F$ does not have a derivative at $x=0.5$
• The graph does not and cannot show the precise behavior of the function near $x=0.5$.  
• The point $\left( 0.5,1 \right)$ is on the graph, because the definition of $F$ says that $F(x)=2x$ for $x$ between $0$ and $0.5$ inclusive.
• For any point $x$ to the right of $0.5$, $F(x)=3{{\left( x-1 \right)}^{2}}$.
• $\underset{x\to {{0.5}^{-}}}{\mathop{\lim }}\,F(x)=1$  but $\underset{x\to {{0.5}^{+}}}{\mathop{\lim }}\,F(x)=0.75$.
• Nevertheless, $F(0.5)=1$, not $0.75$.  That implies that $F$ is not continuous at $x=0.5.$
• It would be wrong to say something like: “$F(x)=3{{\left( x-1 \right)}^{2}}$ starting at the first point to the right of $x=0.5$”. There is no "first point to the right of $0.5$."  See density.

Example "Finite"

(1) A function may not be defined by a formula, and (2) it need not involves numbers at all.

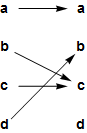
Let the function $F$ be defined on the set $\left\{\textsf{a},\textsf{b},\textsf{c},\textsf{d }\right\}$ like this:  \[F(\textsf{a})=\textsf{a},\,F(\textsf{b})=\textsf{c},\,F(\textsf{c})=\textsf{c},\,F(\textsf{d})=\textsf{b}\] In this definition, $\textsf{a}$, $\textsf{b}$, $\textsf{c}$ and $\textsf{d}$ are letters of the alphabet, not variables.

• $F$ is defined only for inputs $\textsf{a}$, $\textsf{b}$, $\textsf{c}$ and $\textsf{d}$. For example, neither "$F(4)$" nor "$F(\textsf{u})$" are defined.
• I have not defined $F$ using a formula. $F(\textsf{b})=\textsf{c}$ entirely and only because the definition of $F$ says it is.
• You could define $F$ by saying "Let $F$ be defined on the set $\left\{\textsf{a},\textsf{b},\textsf{c},\textsf{d }\right\}$ by the diagram below." That definition gives the same function.
  
  This diagram is called the cograph of the function.
• Databases involve many functions that don't involve numbers. For example the personnel database of a company will likely contain a function that takes the name of each employee to their job title.

The article Representations of functions describes how to represent finite functions in much more detail.

Example: "Word Length"

The domain and codomain of a function can be completely different sets.

Let $S$ be some set of English words, for example the set of words in a given dictionary. Then the length of a word is a function; call it $L$.

• $L$ takes English words as inputs.
• $L$ outputs the number of letters in the word.  For example, $L('\text{cat}')=3$ and $L('\text{polysyllabic}')=12$.
• The method of computation for this function is: count the number of letters. In a computer program, an English word would be stored as a list of characters, and most any computer language has a command that returns the length of a list.

Example: "$n$th pair of primes"

You can correctly define a function you know you can't calculate.

A prime pair consists of a pair of primes that differ by $2$. The first six prime pairs are $(3,5)$, $(5,7)$, $(9,11)$, $(11,13)$, $(17,19)$ and $(29,31)$.

Let $PP:\mathbb{N}\to\mathbb{N}\times\mathbb{N}$ be defined like this: (1) If there are fewer than $n$ prime pairs, then $PP(n)=0$. (2) Otherwise, $PP(n)$ is the $n$th prime pair in order.

• For example $PP(6)=(29,31)$.
• It is not known whether there is only a finite number of prime pairs or an infinite number.
• The largest prime pair known has order of magnitude $10^{19}$. We do not know the value of $n$ for which this number is $PP(n)$.
• So for very large numbers $n$ we know that we do not know how to calculate $PP(n)$. Nevertheless, $PP$ is a perfectly well-defined function.
• There is more information about prime pairs in the Mathworld article Twin primes and in the Wikipedia article Twin primes.

Example: "Dirichlet”

A real-valued function may not have a graph you can draw.

This example uses the concepts of rational and irrational.

Let $F:\mathbb{R}\to\mathbb{R}$ be defined by \[F(x):= \begin{cases} 1 & \text{if }x\text{ is rational}\\ \frac{1}{2} & \text{if }x\text{ is irrational}\\ \end{cases}\]  for all real $x$.

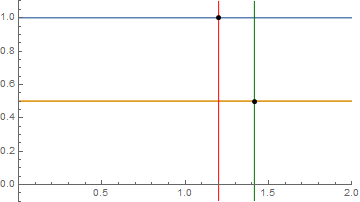
• $F$ is called the Dirichlet function.
• $F(1/3)=1$, $F(-42)=1$, but $F(\pi)=\frac{1}{2}$ because $\pi$ is not rational.
• $F$ is not continuous.

• The "graph" above is completely misleading. Both horizontal lines are full of holes.
• The point $(\sqrt{2},\frac{1}{2})$ is missing from the top line because $\sqrt{2}$ is not rational.
• The point $(1.2,1)$ is missing from the lower line because $1.2=\frac{12}{10}$, which is rational.
• This means that the left vertical line does not intersect the lower line and the right vertical line does not intersect the top line.
• The "graph" is worse than that.
• Both lines are missing infinitely many points.
• No matter how much you magnify either line, you will not see any of the holes, because no matter how small a nonzero distance you name -- call it $\epsilon$ -- there is a point that is on the line that is closer than $\epsilon$ to the hole.
• There is also a hole closer than $\epsilon$ to any point that is on the line.
• See Density of the rationals and Density of the reals.
• You can read more about this function in the Wikipedia article Dirichlet function.

Example: Sine Blur

The graph of a real valued function on a finite interval can be an infinitely long curve.

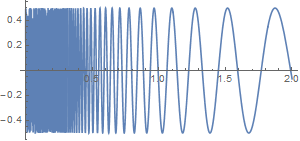
Let $F(x):=.5 \sin \left( \frac{50}{x} \right),\,\,\,\,\,\,\left( x \gt0 \right)$.

• The frequency of the curve goes up rapidly as you get close to the $y$-axis from the right, since $\frac{50}{x}$ grows very rapidly as $x$ moves toward $0$.
• Drawing the graph near the $y$-axis is impossible because the curve between $x = 0$ and any larger number is infinitely long even though it occurs in a finite interval.
• More about this function.

Example: Derivative

A function can have a function as input and a function as output.

Let $\mathcal{D}$ be the set of all differentiable functions from $\mathbb{R}$ to $\mathbb{R}$, and $\mathcal{A}$ the set of all functions from $\mathbb{R}$ to $\mathbb{R}$. Define $D:\mathcal{D}\to\mathcal{A}$ be the function that takes a function $f$ in $\mathcal{D}$ (in other words a function that has a derivative) to its derivative.

• If $f(x):={{x}^{2}}$ then $\text{D}(f)(x)=2x$. Using barred arrow notation, $D(x\mapsto {{x}^{2}})=x\mapsto 2x$.
• If $f(x):=\sin x$ then $\text{D}(f)(x)$ is $x\mapsto\cos x$, in other word $D(x\mapsto\sin x)=x\mapsto\cos x$.
• D takes a function as input and outputs another function, namely the derivative of the first one.  The whole function is the input, not some value of the function, not the rule that defines the function, not the graph.  You have to think of the function as a single thing, in other words as a math object.
• Functions whose inputs are complicated structures such as functions may be called operators .  (Usage varies in different specialties.)  This function $D$ is the differentiation operator.
• The differentiation operator is not injective.  For example, $f(x):={{x}^{2}}$ and $g(x):={{x}^{2}}+42$ have the same derivative, namely $2x$.

The chapter Derivatives contains many graphs, each showing a function and several of its derivatives.

Appendix

Other consciousness-expanding examples of functions

• The Ackermann function.
• Space-filling curves

This work is licensed under a Creative Commons Attribution-ShareAlike 2.5 License.