Produced by Charles Wells Revised 2017-03-01 Introduction to this website website TOC website index blog Back to head of Functions chapter
Contents |
By "images and metaphors" I am referring to the conceptual metaphors that mathematicians use in thinking about mathematical objects. Below are some references for images, metaphors and related ideas:
The illustrations were created using the Mathematica Notebooks Functions and Shapes.nb, FunctionDigraphForImMetFuncs.nb, and AnotherFamiliesFrozen.nb. These notebooks contain many more examples of the ways functions can be represented than are given in this article. For information about how to use them, read the abmath section Mathematica.
Like everything on abstractmath.org, the notebooks are covered by a Creative Commons ShareAlike 3.0 License.
This concept is discussed in Specification and Definition of Function as well as here.
An integer can be odd, or a prime. A triangle can be isosceles, or obtuse. Like any math object, a function can have properties too.
You can bisect an angle or add two numbers. In the same way you apply operations to functions.
Let $f(x):=2\sin^2x-1$ and $g(x):=x^2+2x-8$.
One of the most powerful tools of math is the concept of function space. A function space is a set whose elements are functions (not the values of the functions, the functions themselves). In general, a function space will have certain properties that spaces have. For example, in a function space you may be able to talk about the distance between two functions, thinking of each function as a point.
There are many important function spaces on $\mathbb{R}$ (and also on $\mathbb{C}$). They are the objects of study of functional analysis. But other kinds of sets of functions are studied in math: One example is the set of computable functions on $\mathbb{N}$ in computer science and logic.
Our function $g$ above could be define by any of the following formulas (and zillions of others):
All of those functions give the same answer for any number $x$ you plug into them (including complex numbers). So all the formulas define the same function.
For our function $g$,
The expression $g(x):=x^2+2x-8$ defines a function $g$ from $\mathbb{R}$ to $\mathbb{R}$. The expression "$x^2+2x-8$" is an algebraic expression and as such it can be evaluated for any real number $x$. You can use the expression "$x^2+2x-8$" to carry out a process of computing the value.
The process that is "encapsulated" is not completely determined, but one way or another essentially the same computations are carried out.
A function defined by a table has a process for computing a value, too: Look it up in the table!
This is not just cute remark:
$\pi(n)$, the $n$th prime function, can be computed by finding the first prime, finding the second prime, and so on until you get to $n$. Of course this is ridiculously tedious, but it is a process. You can also evaluate $\pi(n)$ on a computer, for example in Mathematica or Maple. These systems use a built-in process that is more efficient than finding one prime after another.
You could look up the value of a function given by a table this way, too: Start at the top and go down. But people avoid doing that, as mentioned above. Do you remember singing the alphabet song as a child? Now you know why that song exists: to avoid starting at the top.
An algorithm may be used to compute the value of a function.
The algorithms for arithmetic originated in India. They were originally what the word "algorithm" referred to. The word is named after the Persian mathematician Al-Khwarizmi, who popularized them. In the thirteenth century, Fibonacci wrote a book that introduced the algorithms to Europe.
This is a metaphor that seems to occur in many different contexts, and the notation and terminology is all over the place, although words such as transformation and transform are used for specific types of functions.
This example is grossly oversimplified.
The heat $h$ in a room (as shown by a particular thermometer) may depend on the setting $t$ of a thermostat. In this case, $h$ depends on $t$. You could estimate the specific value of $h$ for a given thermostat setting $t$ by setting the thermostat at $t$ and waiting until the temperature shown by the thermometer stabilizes. But you don't have a formula for $h$.
The differential equation \[x'(t)=x(t),x(0)=1\] determines a dependent variable $x$ that depends on an independent variable $t$. In fact, $x(t)=e^t$ for this equation. Nevertheless, the differential equation completely determines the function by giving only two specific facts about $x$ and $\frac{dx}{dt}$. This is significant because in practice many differential equations cannot be solved in terms of functions already known. The Fresnel function is an example.
The following is a story I made up which probably bears some resemblance to what actually happened.
In the early nineteenth century, Augustin-Jean Fresnel studied the theory of optics. He came up with this differential equation: \[y'(t)=\sin \left(\frac{\pi t^2}{2}\right),\ \ \ y'(0)=0\]
The theory for this type of differential equation (which is typically the first type of differential equation you study in college) says that such an equation has a unique solution. The solution of a differential equation is a function, not a number. In this case, the solution gives $y(t)$ as a function of $t$. Its graph looks like this:
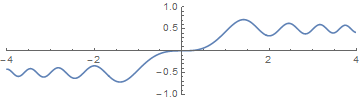
In fact there is a formula for this solution: \[x(t)=\int_0^t\sin\left(\frac{\pi t^2}{2}\right)\,dt\] This integral defines a specific function of $t$, since $\sin\left(\frac{\pi t^2}{2}\right)$ is a continuous function. However, the integral of this function cannot be expressed in terms of functions familiar to you from calculus class. (You can't "do" the integral.) Nevertheless, it is a genuine function and nowadays it has a name: \[\text{FresnelS}(t):=\int_0^t\sin\left(\frac{\pi t^2}{2}\right)\,dt\] Giving it a name doesn't tell you how to calculate this function. Fresnel probably calculated values of the function using its power series.
A symmetry is (roughly speaking) a way of changing an object so that it looks exactly the same after it is changed as before.
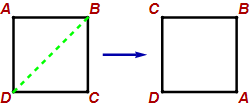
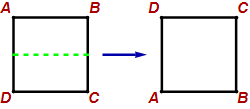
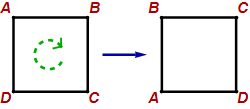
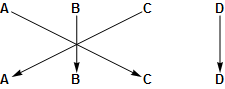
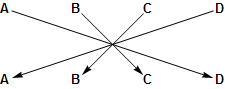
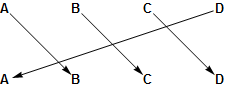
Below are three symmetries of a square. In each case the square is moved as shown. The labels show what the movement did to the corners. The symmetry moves the sides so that each side connects the same two corners. The labels are not part of the square.

There are eight symmetries of a square altogether, including the identity symmetry that leaves the square alone. These symmetries constitute the Dihedral group of order $8$.
Each symmetry can be represented in several different ways as permutations (bijective maps) of its corners. Representations of permutations are also presented in Representations of discrete functions.
These three symmetries may be represented as tables:
Diagonal flip: $\scriptstyle\begin{pmatrix} A&B&C&D\\ C&B&A&D \end{pmatrix}$
Horizontal flip: $\scriptstyle\begin{pmatrix} A&B&C&D\\ D&C&B&A \end{pmatrix}$
Clockwise quarter turn: $\scriptstyle\begin{pmatrix} A&B&C&D\\ B&C&D&A \end{pmatrix}$
![]()
![]()
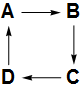
All permutations of finite sets behave the way these do: The endograph is a union of disjoint cycles.
The disjoint cycle notation for permutations is particularly well adapted to composing permutations by hand.
Diagonal flip: $(A C)(B)(D)$
Horizontal flip: $(A D)(B C)$
Clockwise quarter turn: $(A B C D)$
This notation is intended be read this way: If $x$ has a parenthesis to its right, then $p(x)$ is the first symbol in the same parenthesized group, otherwise $p(x)$ is the next symbol to the right in the group. So given the permutation $p=(132)(8)(5467)$, $p(1)=3$, $p(2)=1$ and $p(8)=8$.
The idea that a function is a map
is one of the most powerful metaphors in mathematics.
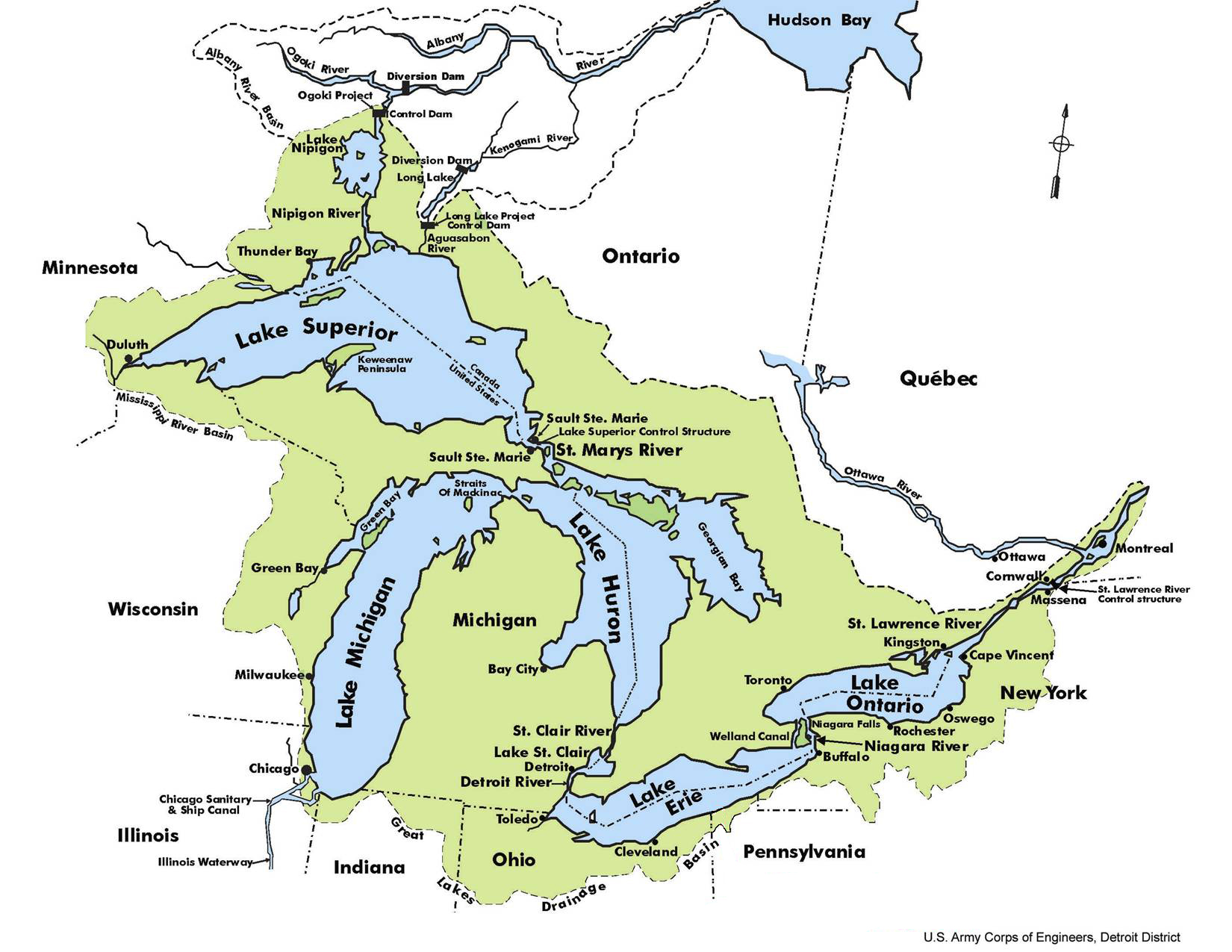
This map is not a function, it is a physical object. But it is modeled as a mathematical function in this way:
The mathematical function corresponding to the map takes a point on the boundary of Michigan (for example) in the real world to a point on your screen. A blue point on the screen is a value of the function at a point in some actual real-world lake. All this is an idealization of the real map, which is necessarily only approximate.
Mapping the Earth's surface comes with lots of math dating back hundreds of years. Much of the work comes from the fact that a mathematical map from a sphere to a plane cannot simultaneously preserve both area and angles.
A decent physical map is more than continuous (taking nearby points on the Earth to nearby points on the screen):
What mathematicians call "maps" are not necessarily geographical maps. In math, we use the word "map" by analogy with the kind of map you see in an atlas:
If a mathematician calls a particular function a map,
then it preserves some property or structure or shape
that the mathematician is interested in.
The examples below illustrate some functions from the plane to itself that preserve area or angles but not both. In fact, a function from the plane to itself can preserve area and angles simultaneously (any rotation with determinant $1$ and any translation will do that), but a map from a sphere to a plane cannot do both at once.
Any matrix with determinant $1$ preserves area. In each example, the function is $(x,y)\mapsto M.{x\choose y}$, where $M$ is the matrix shown. The diagram shows what the function does to three specific shapes.
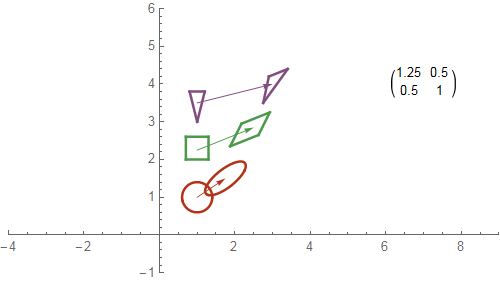
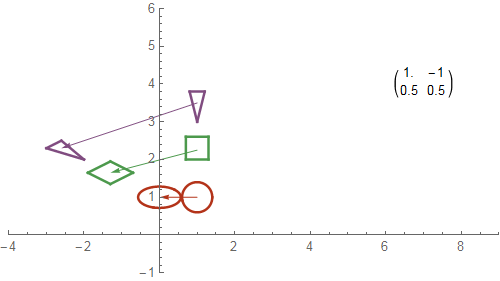
Any rotation matrix preserves angles. Such a function is called conformal.
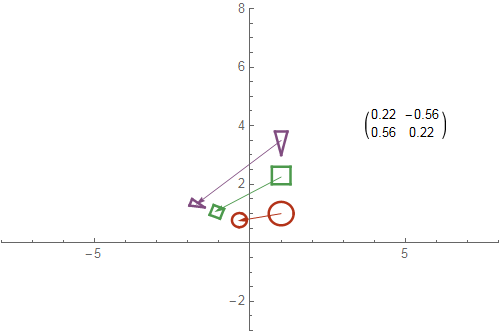
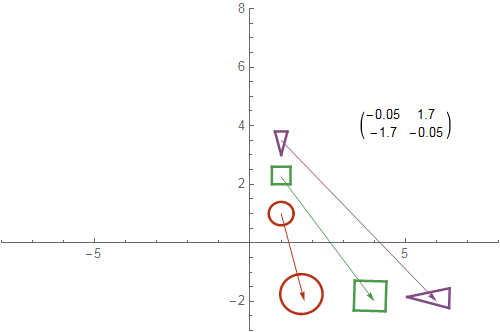
There are more of these pictures in the Mathematica site on abstractmath.org. The pictures of angle-preserving functions are called epf#.gif or EqAng#.gif, where # is a digit, and the cographs are at epf#eg.gif or apf#ed.gif.
The Mathematica Demonstrations Project has many examples of linear transformations.
A structure-preserving function is often called a map, because it "preserves" something of interest the way a physical map does. Two examples of this are given in the section on maps.
The notion of "preserves" is typically defined separately for different types of structure. A function that preserves an algebraic operation (as in the example immediately below) is called a homomorphism. Other words are used for other structures. It is also common to call any particular structure-preserving function a morphism.
Let's define a function $h:\mathbb{R}\to\mathbb{R}$ by $f(x)=2x$. Now do some basic algebra: For any real numbers $r$ and $s$, \[h(r+s)=2(r+s)=2r+2s=h(r)+h(s)\] For example, \[h(3+5)=h(8)=16\] and \[h(3)+h(5)=6+10=16\] We say $h$ preserves the structure of addition on the real numbers. This is typically expressed by the formula \[h(r+s)=h(r)+h(s))\]
It may not be clear why we call addition on the reals a structure. This is because algebra notation hides the structure in a very cramped notation designed to make it easy to do algebra with pencil and paper. We can express addition in a much more open way using trees. (There is more about this in my post Presenting binops as trees.)
The expression "$3+5$" is a symbol that can be exhibited this way:
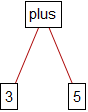
In algebra we evaluate "$3+5$" by writing "$3+5=8$". Let us show this in a much more explicit way:
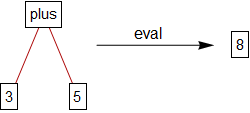
Now I can express the fact that $h$ "preserves addition" using this diagram:
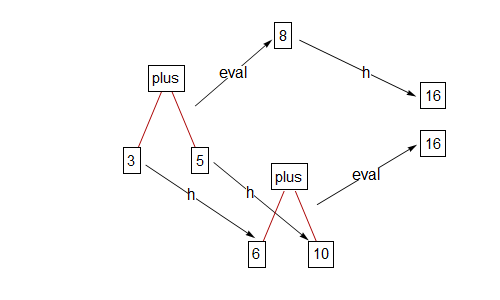
If you start at the left side of the diagram and go to the right over the top, you apply $\text{eval}$ to get $8$, and then you apply $h$ to get $16$. If you go to the right using the lower route, you apply $h$ to each of $3$ and $5$ to get $6$ and $10$, and then you apply $\text{eval}$ to get $16$. Because you get the same thing going over or going under (for any real numbers, not just $3$ and $5$), we say the diagram commutes.
This meaning of the word "commutative" in "commutative diagram" is different from the meaning of the word used in a sentence such as "addition is commutative", meaning $a+b=b+a$. The connection between the two meanings is that in both cases, you can do something in two different ways and get the same answer.
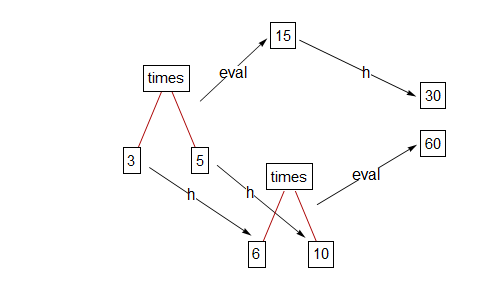
So $h$ does not preserve multiplication.
Structure-preserving maps (morphisms)
occur in every branch of math.
Category theory is an axiomatization of the behavior of structure-preserving maps. It has become quite useful in many branches of math and it has revolutionized some of those branches.
Like all useful axiomatically-defined math structures, categories include objects that are quite different from the phenomena that motivated the definition. In particular, objects in a category don't have to be sets, much less structured sets, and morphisms don't have to be functions at all.
Sources available on line: Logic Matters: Category Theory.
This work is licensed under a Creative Commons Attribution-ShareAlike 2.5 License.