
Produced by Charles Wells Revised 2017-03-28 Introduction to this website website TOC website index blog Back to Understanding Math Chapter head
A mathematical structure is a set (or sometimes several sets) with various associated mathematical objects such as subsets, sets of subsets, operations and relations, all of which must satisfy various requirements (axioms). The collection of associated mathematical objects is called the structure and the set is called the underlying set.
This definition of mathematical structure is not a mathematical definition. The word "structure" is usually used in the definition or discussion of a particular kind of mathematical structure, without any general definition of the phrase "mathematical structure" being given.
In recent times it has become common to define a mathematical structure using either category theory or type theory. Math structures in practice are most commonly defined in terms of (mathematical) spaces, and category theory and type theory makes it easier to give definitions directly in terms of spaces rather than sets. For example, there is a category that is the definition of "group", and a certain kind of functor from it to the category of sets gives a discrete group, a functor to the category of topological spaces gives a topological group, and so on. See Toposes, Triples and Theories, page 125. For a general introduction to this idea, see Shulman, Homotopy type theory: the logic of space.
In this article, I give some simple examples in detail. Although they are simple, they all have uses in one or another branch of math. After those examples, I describe (with links) some mathematical structures of major importance that an undergraduate math student will meet.
$\mathbb{N}$ is the set of all positive integers, $\mathbb{Z}$ is the set of all integers and $\mathbb{R}$ is the set of all real numbers.
A pointed set is a set together with a particular element of the set.
A relation is a set $S$ together with a set of ordered pairs of elements of the set.
I will sometimes denote the set of ordered pairs by a Greek letter, for example $\alpha$ (pronounced "alpha"), so that $\alpha$ must be a subset of $S\times S$. Then, if $(s,s')$ is an ordered pair in the set $\alpha$, you could write "$s\,\alpha\, s'$", pronounced "$s$ is related by alpha to $s'$" or "$s$ alpha $s'$".
The concept that "$\lt$" is a set of ordered pairs takes a bit of getting used to.
There are more examples of relations in the section on Maps between math structures.
Congruence relations are defined by requiring that two integers be related if they have the same remainder when divided by a particular integer. A congruence relation is an example of an equivalence relation.
For example, every integer $n$ leaves one of these remainders when divided by $3$: $0$, $1$ or $2$. I will use the notation "$\underset{3}\sim$" for this relation and similarly for integers other than $3$. (The standard notation is described in the Wikipedia article.) So $5\underset{3}\sim17$ is true because both $5$ and $17$ leave a remainder of $2$ when divided by $3$, but $5\underset{3}\sim10$ is false.
Notice that for integers $m$ and $n$, $m\underset{2}\sim n$ is true if and only if $m$ and $n$ are both even or both odd.
A partition is a set together with a set of subsets (called "blocks") with the property that every element of the set is in exactly one block.
The number of partitions of a finite set is given by the Bell Numbers.

If $S$ and $T$ are sets, then the cartesian product "$S\times T$" is set of all ordered pairs whose first entry is in $S$ and whose second entry is in $T$. In this section we only consider cartesian products with $S=T$.
For example, if $S=\{2,5,7\}$, then \[S\times S=\{(2,2),(2,5),(2,7),(5,2),(5,5),(5,7),(7,2),(7,5),(7,7)\}\]
A binary operation on a set $S$ is a function $b:S\times S\to S$.
A monoid is a binary operation $\Delta:S\times S\to S$ for some set $S$ with two properties given below, using infix notation.
The usual notation for a monoid $\Delta:S\times S\to S$ is "$(S,\Delta)$". $S$ is called the underlying set of the monoid $(S,\Delta)$.
It would be perfectly OK to say simply that $\Delta$ is a monoid, not mentioning $S$. That's because $\Delta$ is a function, and by definition it has to have a domain of the form $S\times S$ for some set $S$. The notation "$(S,\Delta)$" is useful because it gives a name for the underlying set.
Much more detail for monoids is given in the Wikipedia article on monoids. It includes many more examples besides the ones given here.
A math major in a college in the USA is likely to meet with all three of these examples.
A group is an abstraction of symmetry in all of its meanings. The definition of a group says it is a monoid in which every element has an inverse, but the importance of groups comes from their association with symmetry. Most math majors in the USA learn about groups from some course or other.
The Wikipedia articles on groups, symmetries, symmetry groups and group actions include many examples and theorems concerning groups of symmetries.
A vector space is a set, whose elements are called vectors, with an operation of addition on the vectors and an operation called scalar multiplication allowing a vector to be multiplied by a number (or more generally by an element of a particular field).
When you first meet with vectors as a student, typically (in the USA) in second or third semester calculus, they are drawn as arrows; the idea is that a vector is determined by a direction and a length. In that guise they have a basic role to play in physics. In fact, there are vector spaces whose elements are functions; then they are called function spaces and are a major tool in analysis.
The Wikipedia article on vector spaces describes the definition and uses of vector spaces in considerable detail. It is one of the better written math articles in Wikipedia.
A metric space is a set $S$ together with a function $d:S\times S\to\mathbb{R}$ that satisfies a list of axioms that are all true for the distance function on the real line. So a metric space is an abstraction of the behavior of the distance function on the reals. In particular, in a metric space, you can define convergence to a limit.
A metric space is an example of a topological space, although topological spaces are a more general concept.
The Wikipedia article on metric spaces defines metric spaces and gives many examples of them.
Structures of a given type may have maps between them that preserve the structure. Such maps are often called morphisms, but particular types of structures may have their own names for structure-preserving functions. I give some examples here. More examples of structure-preserving maps are given in the article Functions: Images and Metaphors.
If $(S,s)$ and $(T,t)$ are pointed sets, then a function $m:S\to T$ is a morphism of pointed sets if and only if $m(s)=t$.
Suppose $\alpha$ is a relation on $S$ and $\beta$ is a relation on $T$. Then a morphism of relations from $\alpha$ to $\beta$ is a function $f:S\to T$ satisfying the following requirement
If $s\,\alpha\, s'$ then $f(s)\,\beta\,tf(s')$.
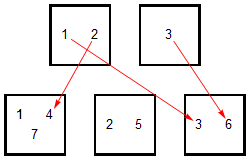
Earlier I mentioned the relation \[\alpha:=\{(1,2),(2,3),(1,3)\}\] on the set $S=\{1,2,3\}$, which is the "less-than" relation "$\lt$" on $S$. Now let $T:=\{1,2,3,4\}$. Then "$\lt$" is also a relation on $T$, namely the relation \[\beta:=\{(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)\}\] Then the function $f:S\to T$ defined by $f(1)=1$, $f(2)=2$ and $f(3)=4$ is a morphism of relations from $(S,\alpha)$ to $(T,\beta)$. The easiest way to check this is by drawing a picture:

In this picture, the less-than relation in each of the sets is simply "above", and you can see that if one number is above another number on the left, then the numbers that the arrows take them to have the same relationship.
A function that preserves the "less-than" relation is called a strictly increasing function. The function that takes $1\to 1$, $2\to 4$, $3\to 4$ does not preserve "$\lt$" since $2\lt3$ but $4$ is not less than $4$. However, that function does preserve the "$\leq$" relation, since $4\leq4$. As you might guess, such a function is called an increasing function but not a strictly increasing function.
Let's look at the doubling function $d:\mathbb{N}\to\mathbb{N}$ defined by $d(n)=2n$.
The function $d$ is a morphism of relations from $\underset{3}\sim$ to $\underset{2}\sim$. To prove this requires showing that if $m\underset{3}\sim n$, then $2m\underset{2}\sim 2n$. Now, by definition, for any integers $r$ and $s$, $r\underset{2}\sim s$ means that $r$ and $s$ are both even or both odd. But for any integer $r$, $2r$ is always even! So the statement "If $m\underset{3}\sim n$, then $2m\underset{2}\sim 2n$" is true because "$2m\underset{2}\sim 2n$" is always true!
If you are not sure you understand this, read about the truth table for conditional assertions: If $Q$ is true, then "If $P$ then $Q$" is always true.
On the other hand, $d$ is not a morphism of relations from $\underset{2}\sim$ to $\underset{3}\sim$. This is false by counterexample: $4\underset{2}\sim 8$ because they are both even, but $8\underset{3}\sim 16$ is false, because when $8$ is divided by $3$ the remainder is $2$, whereas when $16$ is divided by $3$ the remainder is $1$.
Let $S$ and $T$ be sets and $P_S$ be a partition of $S$ and $P_T$ a partition of $T$. A function $f:S\to T$ is a morphism of partitions if $f$ takes every element of a block of $P_S$ into one particular block of $P_T$.
We looked previously at these two partitions:
Any constant function is a morphism of partitions from $P$ to $Q$, for example this one:
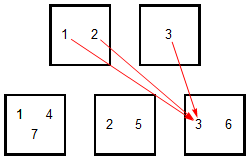
These are also morphisms of partitions:
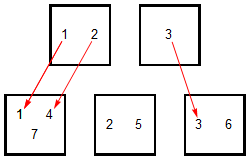
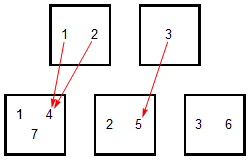
The inclusion function is not a morphism of partitions (in this case!).
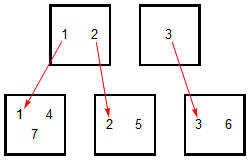
This function is also not a morphism:
Suppose $*$ is a binary operation on a set $S$ and $\#$ is a binary operation on a set $T$. Then a function $f:S\to T$ is a morphism of binary operations if for all $s,s'\in S$, $f(s* s')=f(s)\# f(s')$. The customary way of saying this is: "$f:(S,*)\to(T,\#)$ is a homomorphism from $(S,*)$ to $(T,\#)$".
Many examples of morphisms of binary operations are described in the abstractmath.org article Functions: Images and Metaphors. I will give one example here.
Both addition and multiplication are binary operations on the set $\mathbb{R}$ of real numbers. Let $E:\mathbb{R}\to\mathbb{R}$ be the function defined by $E(r):=2^r$. Then $E:(\mathbb{R},+)\to(\mathbb{R},\times)$ is a homomorphism.
This follows from the law of exponents: \[E(r+s)=2^{r+s}=2^r\times 2^s=E(r)\times E(s)\]
Suppose $(S,\Delta)$ and $(T,\nabla)$ are monoids with identities $e_S$ and $e_{T}$. Then a function $h:S\to T$ is a homomorphism if \[\text{(ME)}\,\,\,\,\,\,\,\,h(e_S)=e_T\] and for all elements $s, s'$ of $S$, \[\text{(MM)}\,\,\,\,\,\,\,\,h(s\Delta s')=h(s)\nabla h(s')\] This is described by saying "$h$ preserves the identity and the binary operation."
The same set can have many different structures on it. For example, a two-element set has two different partition structures on it and sixteen different binary operations on it.
Widely-used mathematical objects generally have "canonical structures" (or "standard" structures) of various types on them. For example, the set of integers can be ordered in many ways, but it has a particular ordering (the familiar one) that is referred to as "the ordering of the integers". This is the ordering that begins $1\lt2\lt3\lt4\ldots$
In the same way, the set of real numbers has a canonical ordering ($r\lt s$ means that there is a positive real number $t$ for which $r+t=s$), a canonical algebraic structure, a canonical metric space structure and a canonical topology.
Presenting a complex mathematical idea as a mathematical structure involves finding a minimal or nearly minimal set of associated objects (a structure) and a minimal or nearly minimal set of conditions on those objects from which the theorems about the structure follow. The ingredients of the structure are kept (nearly) non-redundant so that it is easier to verify that some object is an example of that kind of structure. This is essentially the main use of the axiomatic method
This small set of objects and conditions may not be the most important aspects of the structure for applications or for one's mental representation of the structure.
All this is discussed in more detail in the article on Definition.
The same kind of structure can often be defined by two or more very different kinds of minimal ingredients. A mathematical structure of a given type has lots of structure implied by the minimal definition, and when you think of a structure it is best to think of it as containing all that information, not just the stuff in the definition.
"Equivalence relation" and "partition" are two different ways of defining exactly the same structure on a set. This is explained in the Wikipedia article on The Fundamental Theorem of Equivalence Relations.
This work is licensed under a Creative Commons Attribution-ShareAlike 2.5 License.