Produced by Charles Wells Revised 2017-03-08 Introduction to this website website TOC website index blog head of Functions chapter
Contents |
This chapter provides examples of many different ways of representing discrete functions (almost all of them are finite functions). Many of the representations are visual but some are formulas or expressions.
A discrete set is (informally) a set in which any point has no other point within a certain distance from it: all its points are isolated. In the extreme case, there may not be any notion of distance at all that applies to the set.
Every finite set is a discrete set.
A discrete function is a function whose domain and codomain are discrete sets.
A finite function is a function whose domain is a finite set.
Nearly all the examples in this chapter are finite functions.
A finite function $f:S\to T$ may be represented in these ways:
All these techniques can also be used to show finite portions of infinite discrete functions.
Let \[\text{f}:\{a,b,c,d,e\}\to\{a,b,c,d\}\] be the function defined by requiring that $\text{f}(a)=c$, $\text{f}(b)=a$, $\text{f}(c)=c$, $\text{f}(d)=b$, and $\text{f}(e)=d$. ($a$, $b$, $c$, $d$ and $e$ are all letters of the alphabet, not variables.)
The mathematical graph of $\text{f}$ is the set \[\{(a,c),(b,a),(c,c),(d,b),(e,d)\}\] As with any set, the order in which the pairs are listed is irrelevant. Also, the letters $a$, $b$, $c$, $d$ and $e$ are merely letters. They are not variables.
$\text{f}$ is given by this table:

This sort of table is the format used in databases. For example, a table in a database might show the department each employee of a company works in:

The rule determined by the finite function $\text{f}$ has the form
\[(a\mapsto b,b\mapsto a,c\mapsto c,d\mapsto b,e\mapsto d)\]Rules are built in to Mathematica and are useful in many situations. In particular, the endographs in this article are created using rules. In Mathematica, however, rules are written like this:
\[(a\to b,b\to a,c\to c,d\to b,e\to d)\]This is inconsistent with the usual math usage (see barred arrow notation) but on the other hand is easier to enter when using Mathematica.
In fact, Mathematica uses very short arrows in their notation for rules, shorter than the ones used for the arrow notation for functions. Those extra short arrows don't seems to exist in TeX.
Two-line notation is a kind of horizontal table.
\[\begin{pmatrix} a&b&c&d&e\\c&a&c&b&d\end{pmatrix}\]The three notations table, rule and two-line do the same thing: If $n$ is in the domain, $\text{f}(n)$ is shown adjacent to $n$ -- to its right for the table and the rule, and below it for the two-line.
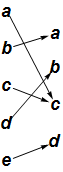
To make the cograph of a finite function, you list the domain and codomain in separate parallel rows or columns (even if the domain and codomain are the same set), and draw an arrow from each $n$ in the domain to $\text{f}(n)$ in the codomain.
This is the cograph for $\text{f}$, represented in columns

and in rows
Pretty ugly, but the cograph for finite functions does have its uses, as for example in the Wikipedia article composition of functions.
In contrast to the table, rule and two-line notation, in a cograph each element of the codomain is shown only once, even if the function is not injective.
In both the two-line notation and in cographs displayed vertically, the function goes down from the domain to the codomain. I guess functions obey the law of gravity.
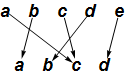
There is no expectation that in the cograph $f(n)$ will be adjacent to $n$. But in most cases you can rearrange both the domain and the codomain so that some of the structure of the function is made clearer; for the function $\text{f}$:
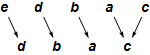
The domain and codomain of a finite function can be rearranged in any way you want because finite functions are not continuous functions. This means that the locations of points $x_1$ and $x_2$ have nothing to do with the locations of $f(x_1)$ and $f(x_2)$: The domain and codomain are discrete.
The endograph of a function $h:S\to T$ contains one node labeled $s$ for each $s\in S\cup T$, and an arrow from $s$ to $s'$ if $h(s)=s'$. Below is the endograph for $\text{f}$.
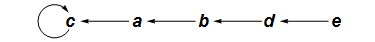
The endograph shows you immediately that $\text{f}$ is not a permutation. You can also see that with whatever letter you start with, you will end up at $c$ and continue looping at $c$ forever. You could have figured this out from the cograph (especially the rearranged cograph above), but it is not immediately obvious in the cograph the way it in the endograph.
There are more examples of endographs below and in the blog post A tiny step towards killing string-based math. Calculus-type functions can also be shown using endographs and cographs: See Mapping Diagrams from A(lgebra) B(asics) to C(alculus) and D(ifferential) E(quation)s, by Martin Flashman, and my blog posts Endographs and cographs of real functions and Demos for graph and cograph of calculus functions.
Suppose $p$ is the permutation of the set \[\{0,1,2,3,4,5,6,7,8,9\}\]given in two-line form by \[\begin{pmatrix} 0&1&2&3&4&5&6&7&8&9\\0&2&1&4&5&3&7&8&9&6\end{pmatrix}\]
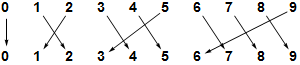
Again, the endograph shows the structure of the function much more clearly than the cograph does.
The endograph consists of four separate parts (called components) not connected with each other. Each part shows that repeated application of the function runs around a kind of loop; such a thing is called a cycle. Every permutation of a finite set consists of disjoint cycles as in this example.
Any permutation of a finite set can be represented in disjoint cycle notation: The function $p$ is represented by:
\[(0)(1,2)(3,4,5)(6,7,8,9)\]Given the disjoint cycle notation, the function can be determined as follows: For a given entry $n$, $p(n)$ is the next entry in the notation, if there is a next entry (instead of a parenthesis). If there is not a next entry, $p(n)$ is the first entry in the cycle that $n$ is in. For example, $p(7)=8$ because $8$ is the next entry after $7$, but $p(5)=3$ because the next symbol after $5$ is a parenthesis and $3$ is the first entry in the same cycle.
The disjoint cycle notation is not unique for a given permutation. All the following notations determine the same function $p$:
\[(0)(1,2)(4,5,3)(6,7,8,9)\] \[(0)(1,2)(8,9,6,7)(3,4,5)\] \[(1,2)(3,4,5)(0)(6,7,8,9)\] \[(2,1)(5,3,4)(9,6,7,8)\] \[(5,3,4)(1,2)(6,7,8,9)\]Cycles such as $(0)$ that contain only one element are usually omitted in this notation.
The article Images and Metaphors for Functions contains more detailed examples of representations of a permutation.
Below is the endograph of a function \[t:\{0,1,2,3,4,5,6,7,8,9\}\to\{0,1,2,3,4,5,6,7,8,9\}\]
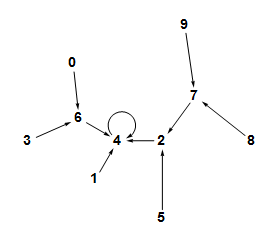
This endograph is a tree. The graph of a function $f$ is a tree if the domain has a particular element $r$ called the root with the properties that
In the case of $t$, the root is $4$. Note that $t(4)=4$, $t(t(7))=4$, $t(t(t(9)))=4$, $t(1)=4$, and so on.
You may complain that I didn't define the function that made the tree above. Well, I don't have to. The tree itself defines the function. All the ways of exhibiting finite functions that I have discussed here tell you exactly what the function is (except in some cases what the codomain is).
The endograph
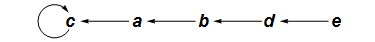
shown above is also a tree.
See the Wikipedia article on trees for the usual definition of tree as a special kind of graph. For reading this article, the definition given in the previous paragraph is sufficient.
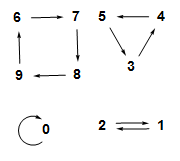
This is the endograph of a function $t$ on a $17$-element set:
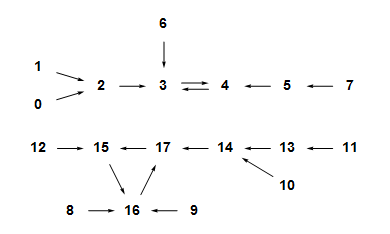
It has two components. The upper one contains one $2$-cycle, and when you apply $t$ over and over to any point in that component, you wind up flipping back and forth in the $2$-cycle forever. The lower component has a $3$-cycle with a similar property.
This illustrates a general fact about finite functions:
In the example above, the cycle in the top component has three trees attached to it, two to $3$ and one to $4$, and the cycle in the bottom component has four trees attached to it.
You can check your understanding of finite functions by thinking about the following two theorems:
This work is licensed under a Creative Commons Attribution-ShareAlike 2.5 License.