abstractmath.org 2.0
help with abstract math

Produced by Charles Wells     Revised 2017-04-09

Introduction to this website    website TOC    website index

blog    Back to head of functions chapter

Properties of functions

Injectivity

Definition

A function $F:A\to B$ is injective if for any elements $a,\,\,a'$ in the domain $A$, if $a\ne a'$ then $F(a)\ne F(a')$.

It is the whole function that is or is not injective.

Useful rewordings of the definition:

• $F:A\to B$ is injective if and only if for all $a,\,\,a'\in A$, if $F(a)=F(a')$ then $a=a'$. This is the contrapositive of the definition, and so is equivalent to it.  In many cases this is the best version of the definition to use in a proof.
• $F:A\to B$ is injective if and only if "different inputs give different outputs", or in another wording, if and only if "different elements of $A$ go to different elements of $B$."

Usage

To say "$F$ is injective", you can also say

• $F$ is one-to-one.
• $F$ is an injection.
• $F$ is monic.

Warning:  Do not try to reword this definition
using the word "unique".
It is too easy to get it mixed up with
the definition of functional property.

This is explained in the article on dysfunction.

Examples

• The identity and inclusion functions are injective.
• The constant function $k:\mathbb{R}\to\mathbb{R}$ for which $k(x)=3$ for all $x\in\mathbb{R}$ (in other words the function $x\mapsto 3$) is not injective, since for example $k(0)=k(\pi)=k(42)=3$.
• On the other hand, the function $x\mapsto 4:\{4\}\to\{4\}$ is injective, since the domain $\{4\}$ has only one element, so "different elements go to different elements" vacuously because the domain does not have two different elements.
• The doubling function $x\mapsto 2x$ is injective on the real numbers and in fact on the complex numbers, because doubling different numbers gives different numbers.

• The squaring function $x\mapsto {{x}^{2}}$ is not injective, because for example ${{2}^{2}}={{(-2)}^{2}}$:  Squaring two different numbers can give you the same number.
• The cubing function on the reals is injective.  It is not injective on the complex numbers, because for example                \[{{2}^{3}}={{(-1-i\sqrt{3})}^{3}}={{(-1+i\sqrt{3})}^{3}}=8\]

Properties of injective functions

Horizontal line crosses the graph only once at most

Let $F:\mathbb{R}\to \mathbb{R}$ be a real continuous function.  Then $F$ is injective if no horizontal line cuts the graph of the function twice.  This is a useful way of thinking about injective continuous functions, but it doesn’t work with arbitrary functions. (But see the section below on finite functions.)

Examples

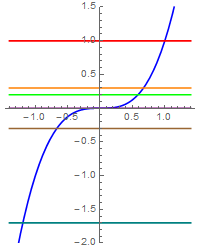
• This is a plot of part of $y=F(x)={{x}^{3}}$ (which is injective) with some horizontal lines. The $x$=axis is one of the lines cutting it. You can't tell just by looking at the graph that the graph isn't horizontal for a short distance along the $x$-axis near zero, but you know from calculus that $F'(x)=3x^2$, which is zero only at zero and nowhere else.
  
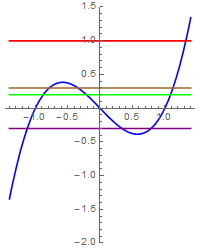
• On the other hand, $G(x)={{x}^{3}}-x$ is not injective.  Note that some horizontal lines cut it more than once, but others cut it only once. 
  
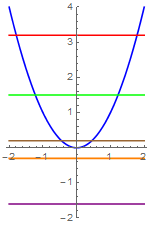
• Horizontal lines don’t have to cut a function at all.  The graph below is part of $y={{x}^{2}}$.  Horizontal lines below zero don’t cut its graph because $0$ is its minimum.  There are horizontal lines that cut it twice, so it is not injective. Note that the $x$-axis cuts the curve exactly once, but that does not change the fact that the function is not injective because other lines cut it twice.
  

No information loss

An injective function $F:A\to B$ loses no information.  If you have an output from the function, you know it came from exactly one input.

•  If you got $8$ when you cubed a real number, the real number had to be $2$.  The cubing function is injective on the reals, as shown previously. But if you got $8$ when you cubed a complex number, the complex number could be any of three numbers; the cubing function is not injective on the complex numbers.
• If you got $4$ when you squared something, the something could have been either $2$ or $-2$:  You lost some information about the input, namely its sign in this case.  The squaring function is not injective.

• If you get $\frac{1}{2}$ as an output from the sine function, it could have come from any one of an infinite number of inputs.  The sine function is ridiculously noninjective: $\sin t=\frac{1}{2}$ if and only if $t=\frac{\pi}{6}+2n\pi$ or $t=\frac{5\pi}{6}+2n\pi$ for any integer $n$.
  

Surjectivity

Definition

A function $F:A\to B$ is surjective if and only if for every element $b$ in the codomain B there is an element $a$ in the domain $A$ for which $F(a)=b$.

Useful rewordings of the definition:

• $F:A\to B$ is surjective if and only if the image of $F$ is the same as the codomain $B$.
• $F:A\to B$ is surjective if and only if every element of $B$ is the value of some element of $A$.
• More informally, $F:A\to B$ is surjective if and only if every element of $B$ "comes from" some element of $A$.

Usage

Another way of saying that $F:A\to B$ is surjective is to say "$F$ is onto" or "$F$ is onto $B$."

Examples

• Identity functions are surjective.
• An inclusion function $i:A\to B$ is surjective if and only if $A=B$ (in which case it is the identity function!). For example, the inclusion of $\{1,2\}$ into itself is surjective, but the inclusion of $\{1,2\}$ into $\{1,2,42\}$ is not surjective, because $42$ does not "come from" an element of $\{1,2\}$.
• Let $F:\mathbb{R}\to \mathbb{R}$ be the squaring function, so $F(x)={{x}^{2}}$ for every real number $x$.  Then $F$ is not surjective, since for any negative number $b$, there is no real number $a$ such that $F(a)=b$. (You can’t solve ${{x}^{2}}=-2$, for example).
• But if you define $G:\mathbb{R}\to {{\mathbb{R}}^{+}}$ (where ${{\mathbb{R}}^{+}}$ denotes the set of nonnegative reals) by $G(x)={{x}^{2}}$, then $G$ is surjective.  As you can see, whether a function is surjective or not depends on the codomain you specify for it.   Note that "$G$ is surjective" says exactly that every nonnegative real number has a square root.

Every horizontal line crosses the graph at least once.

A function $F:\mathbb{R}\to \mathbb{R}$ is surjective if every horizontal line crosses its graph one or more times. You can check the following properties by looking at the graphs above:

• $x\mapsto x^3:\mathbb{R}\to \mathbb{R}$ is surjective.
• $x\mapsto x^3-x:\mathbb{R}\to \mathbb{R}$ is surjective.
• $x\mapsto x^2:\mathbb{R}\to \mathbb{R}$ is not surjective.
• $x\mapsto \sin x:\mathbb{R}\to \mathbb{R}$ is not surjective.

However, $x\mapsto x^2:\mathbb{R}\to \mathbb{R}^+$ and $x\mapsto \sin x:\mathbb{R}\to [0,1]$ are surjective. ($[0,1]$ is the closed interval $\{x\in\mathbb{R}|-1\lt x\lt 1\}$.)

Bijectivity

Definition

A function that is both injective and surjective is said to be bijective.

Usage

A bijection $F:A\to B$ matches up the elements of $A$ and $B$ -- each element of $A$ corresponds to exactly one element of $B$ and each element of $B$ corresponds to exactly one element of $A$. For this reason, a bijection is also called a one-to-one correspondence.

Examples

• Any identity function is bijective.
• If $A$ is a subset of $B$ and $A\neq B$ (we say $A$ is a proper subset of $B$) then the inclusion function $\text{inc}:A\to B$ is injective but is not bijective.
• The function $x\mapsto x^3:\mathbb{R}\to\mathbb{R}$ is bijective, but the other functions shown in the graphs above are not bijective.

Properties of finite functions

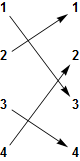
You can see whether a finite function is injective, surjective or both by looking at its cograph.

Examples

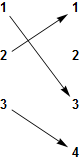
• This function is bijective:
  
• This is injective but not surjective (there is an element of the codomain with no arrow pointing to it):
  
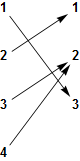
• This is surjective but not injective (there is an element of the codomain with more than one arrow pointing to it):
  
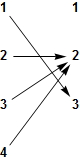
• This is neither injective nor surjective:
  

This work is licensed under a Creative Commons Attribution-ShareAlike 2.5 License.