abstractmath.org 

GLOSSARY  

 

Posted 23 October 2009

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

 

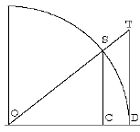tangent

The word tangent may refer either 

¨      to a straight line in a certain relation to a differentiable curve, or

¨      to a certain trigonometric function.

These two meanings are related: the trigonometric tangent of an angle (SOC in the picture) is the length of a certain line segment (TD in the picture) tangent to the circle of radius 1.

term

The word term is used is several ways in math English.

A constituent of a sum or sequence

A term is one constituent of a sum or sequence (finite or infinite), in contrast to a factor, which is a constituent of a product.

Example

The terms in the expression  are , 2x and 1. 

A symbolic expression denoting a mathematical object

¨      This is discussed here.  Note that this use and the preceding one conflict. For example, the expression “  ” contains symbolic terms  and , which would in math English be called factors rather than terms. 

 

In terms of

Writing a function in terms of x means giving a defining equation containing x as the only variable.  (but it may contain parameters).

Example

The expression  implicitly determines y in terms of x.  Explicitly, y is given in terms of  x by .

TFAE

Abbreviation for "the following are equivalent".

that is

Indicating equivalence

The phrase "that is" may be used to indicate that what follows is equivalent to what precedes, usually when the equivalence is essentially a rewording.

Examples

¨      "We have shown that xy < 0, that is, that x and y are nonzero and of opposite sign."

¨      "Then n = 2k, that is, n is even."

Indicating significance

"That is" is sometimes used in the situation that what after is an explanation of the significance of what comes before. The explanation may be a rewording as above, so that these two usages overlap.

Example

"If the function is a polynomial, that is, easy to calculate, numerical estimates are feasible."

the

The word "the" is called the definite article. It is used in forming definite descriptions: phrases that describe a particular individual.  The particular individual is often known from context.  If you hear someone say “I saw the boy we talked to the other day” the speaker expects the listener to know what the speaker means.  If they say “I saw a boy with a straw hat”, the speaker does not expect the listener to know what they mean (“a boy” is an indefinite description).  Definite descriptions can also be formed with “this” and “that”. 

The definite article as universal quantifier

In math English, both the indefinite article and the definite article can have the force of universal quantification. Examples are given under universal quantifier. 

The definite article and setbuilder notation

A set  is often described in setbuilder notation with a phrase such as "the set of  x such that P(x)". In particular, this set is the set of all  x for which P(x) is true..

Example

The set described by the phrase "the set of even integers" is the set of all even integers.  Beginners in abstract math classes sometimes miss this.  To the question

"Let  E be the set of even integers. Show that the sum of any two elements of  E is even."

students have given answers such as this:  

"Let E = {2,4,6}. Then 2 + 4 = 6, 2 + 6 = 8 and 4 + 6 =10, and  6,  8 and 10 are all even."

This answer is wrong, because E is not the set of all even integers. 

Definite article in definitions

The definiendum of a definition may be a definite description.

Example

"The sum of vectors   and  is  ."

The word “the” can make you believe that you should know what it refers to.   More about this here.

there is

then

theorem

To call an statement a theorem is to claim that the statement has been proved.

Remark

In texts the proof is usually given after the theorem has been stated. In that case (assuming the proof is correct) it is still true that in real time the theorem "has been proved"!   

Some authors refer only to assertions they regard as important as theorems, and use the word proposition for less important ones. See also lemma and corollary.

Theorems, along with mathematical definitions, may be set off in the text with a box or a different typeface.

theory of functions

In older mathematical writing, the phrase theory of functions refers by default to the theory of analytic functions of one complex variable.

 

 

tilde

transformation

trigonometric functions

Degrees and radians

If you write “sin x” meaning the sine of x degrees, you are not using the same function as when you write “sin x”, meaning the sine of x radians. They have different derivatives, for example:  Let sin x denote the sine of x radians and sind x the sine of x degrees, so that .  Then  but .

The same remark may be made of the other trig functions.  In postcalculus pure mathematics “sin x” nearly always refers to the sine of x radians, often without explicitly noting the fact. This is not true for texts written by non-mathematicians, who at least often use the degree sign to tell you.

Variations in usage

¨      In the USA you calculate the sine function on the unit circle by starting at (1, 0) and going counterclockwise: the sine is the projection on the y-axis.  In some other countries (for example, Hong Kong secondary schools) you may start at (0,1) and go clockwise (the sine is the projection on the x-axis).  I learned this from students. 

¨      Students educated in Europe may not have heard of the secant function; they would simply write .

¨      You usually write evaluation of trig functions by juxtaposition (with a small space for clarity), thus:  sin x instead of sin(x). Students sometimes read this as multiplication.

See also logarithm and tangent.   

trivial

About propositions

A theorem is said to be trivial to prove or trivially true

a)    If the theorem follows by rewriting using definitions, or

b)    If the speaker’s mental representation of the mathematical object mentioned in the theorem makes the truth of the fact immediately perceivable.   

Notes

¨      I prefer “obvious” for meaning (b).   “Trivial” is unnecessarily put-downy. 

¨      These definitions are based on my own observation and are not justified by lexicographical citations.

Example

Here is a scenario that exemplifies (a):

¨      A textbook defines the image of a function  to be the set of all elements of B of the form F(a) for some .

¨      It then goes on to say that F is surjective if for every element b of B there is an element  with the property that F(a) = b.

¨      It  then states a theorem, or give an exercise, that says that a function  is surjective if and only if the image of F is B.

¨      The proof follows immediately by rewriting using definitions.

¨      Some students are totally baffled.

¨      The instructor calls the proof trivial and goes on to the next topic.

I have seen this happen several times with this and other theorems.  This sort of incident may be why many intelligent people feel they are “bad at math”. 

Example

Theorem:  Let G be a finite group and H a subgroup of index 2 (meaning it has half the number of elements of the group).  Then H is normal in G.

If part of your basic picture of a group and a subgroup is that the subgroup determines a partition consisting of left cosets and another partition of right cosets, each with the same number of elements as the subgroup, then H having index 2 immediately means that every left coset is a right coset and vice versa, which is equivalent to H being normal.  This exemplifies (b). 

About mathematical objects

A function may be called trivial if it is the identity function or a constant function, and possibly in other circumstances.

A solution to an equation may be said to be trivial if it is 0 or 1.  (This depends on the circumstances.  If someone showed that the cosmological constant is 0  that would not be called trivial.) There may be other situations in which a solution is called "trivial" as well.

A mathematical structure is said to be trivial if its underlying set is empty or a singleton set. In particular, a subset of a set is nontrivial if it is nonempty. I have not found an example where “nontrivial subset” means it is not a singleton.  See also proper.

Remark

"Trivial" and “degenerate” overlap in meaning but are not interchangeable.  What is called “degenerate” semes to depend on the mathematical specialty.

truth value 

The truth value of a statement is “true” if it is true and “false” if it is false.   For example, the truth value of “7 + 3 = 10” is “true” and the truth value of “7 + 3 = 11” is “false”.  Observe that this is in fact a function from the set of statements to the set {“true”, “false”}. 

Assertions with variables in them need not be either true or false.  For example, if n is an integer, the statement “n > 7” is neither true nor false as long as nothing is known about n.  If you know n = 42, then you know that “n > 7” is true.  If you know that n > 4, you still don’t know the truth value of “n > 7”.   In this situation, some authors say the truth value is indeterminate.

two

In mathematical discourse, two mathematical objects can be one object!  This is because two identifiers used for them usually are allowed to have the same value unless some word such as “distinct” is used to ensure that they are different.

Examples

¨      "The sum of any two even integers is even".  In this statement, the two integers are allowed to be the same.   It is true in any case. 

¨      “The difference of any two distinct even integers is a nonzero even integer.”  This statement is true but it requires the word “distinct”.  Many mathematicians, including me, would regard the statement with “distinct” omitted as either false or badly written.

¨      Another example occurs under transitive.

Wikipedia’s definition of boolean algebra said until recently that a boolean algebra has “…two elements called 0 and 1…”  It did not say they must be distinct in the axiom but in the examples it said that the two-element boolean algebra is the simplest example.  (It says “distinct” now  18 October 2006.)

type