 abstractmath.org
abstractmath.org
GLOSSARY
Posted 26 July
2008
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
a, an
|
The articles in English
are the indefinite article "a"
(with variant "an") and the definite
article "the". If your
native language is not English you may have problems understanding some mathematical
discourse because the articles are used in English in some fairly subtle
ways. This is explained in a handout from |
The word "a" or "an" is the indefinite article,
one of two articles in English.
Generic use
In math writing, the indefinite article may be used with the name of a
type of math object (producing an indefinite description a description not meant to refer to an
instance of the object that has been previously referred to) to indicate an
arbitrary object of that type. Note that plural indefinite descriptions do not
use an article.
Example
"Show that an integer that is divisible
by four is divisible by two."
¨ Correct interpretation: Show that every integer that is
divisible by four is divisible by two.
¨ Incorrect
interpretation: Show that some
integer that is divisible by four is divisible by two.
So in a sentence like this it the indefinite article has the
force of a universal quantifier. Unfortunately, this is also true of the
definite article in some circumstances!
More examples are given in the entry on universal quantifier.
Generic only in subject
An indefinite description has the force of universal
quantification when it is the subject of the clause.
Consider:
¨ "A number
divisible by 4 is even." (Subject of sentence.)
¨ "Show that a
number divisible by 4 is even." (Subject of subordinate clause.)
¨ "Problem: Find
a number divisible by
Difference with ordinary English
In ordinary English sentences, such as a
"A wolf takes a mate for life."
the meaning is that the assertion is true for a typical individual (typical wolf in
this case). In mathematics, however, the assertion is required to be true without exception.
abstract algebra
See algebra.
abuse of notation
Notation may be called abuse of notation if it involves
¨ identifying two structures along an isomorphism between them.
Click on those entries for examples.
The word “abuse” makes it sound worse than it really is. Without judicious use of this technique much mathematical writing would be unreadable.
aleph
Aleph is the first letter of the Hebrew alphabet,
written .
It is the only Hebrew letter used widely in mathematics. Its most common use is to refer to infinite cardinals.
algebra
This word has many different meanings in the school system
of the
High school algebra is primarily algorithmic and concrete in nature. This is where you learn to solve linear and quadratic equations (MW, Wik) and to apply them using word problems.
College algebra is the name given to a college course, perhaps remedial, covering the material covered in high school algebra.
Linear algebra may be a course in matrix theory (MW, Wik) or a course in linear transformations in a more abstract setting.
A college course for math majors called algebra, abstract algebra, or perhaps modern algebra, is an introduction to groups, rings, fields and perhaps modules (MW, Wik). It is for many students the first course in abstract mathematics and may play the role of a filter course. In some departments, linear algebra plays the role of the first course in abstraction.
Universal algebra (MW, Wik) is a subject math majors don't usually see until graduate school. It is the general theory of structures with n-ary operations subject to equations, and is quite different in character from abstract algebra.
algorithm
The word algorithm is used in three confusingly similar ways:
algorithm as process
Mathematicians typically use the word “algorithm” for a step by step process for calculating something,
as for example the procedure expressed roughly by the description below.
People who use the word “algorithm” in this
way may refer to a program implementing it as the code for the algorithm.
algorithm as program
A program may itself be called “an algorithm”. In my experience, this is not common usage.
algorithm as mathematical object
In computer science or logic texts, the word “algorithm” may
be given a mathematical
definition (for example as a Turing machine (MW,
Wik)),
turning an algorithm into a mathematical object.
Example
You can write a
program in Pascal and another one in C to take a list with
at least three entries and swap the second and third entries. There is a sense
in which the two programs, although different as programs, implement the “same” algorithm (process): Change
to
.
Example
(NM) “Start with a guess x
and let (see colon-equals)
repeatedly until either
¨
f(x) gets
sufficiently close to
¨
,
or
¨ the process has gone on too long.”
This algorithm is not hard to implement in C, Pascal,
Fortran or many other programming languages.
But in all these cases you have to get the syntax exactly right and take
care of a lot of details such as assigning labels to certain lines of the
program. Note that (NM) is not any of those programs: it is the process carried out by those
programs.
The different
meanings of “algorithm” are discussed with examples in the Wikipedia. For a detailed development of formal
algorithms, see Introduction to Automata Theory, Languages and Computation, by
J. E. Hopcroft and J. D. Ullman, Addison-Wesley,
See also the discussion of functions here.
alias
The symmetry of the square illustrated by the figure below can be described in two different ways.
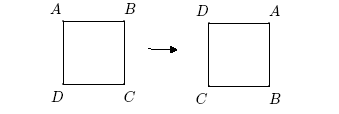
¨ The corners of the square are relabeled, so that what was labeled A is now labeled D. This is called the alias interpretation of the symmetry.
¨ The square is turned, so that the corner labeled A is now in the upper right instead of the upper left. This is the alibi interpretation of the symmetry.
“Alibi” and “alias” are not mathematical properties of transformations, but ways to think about them.
all
See universally true and universally true conditionals.
always
See universal quantifier.
ambient
The
word ambient is used to refer to a mathematical
object such as a space that contains a given mathematical object.
It is also commonly used to refer to an operation on the ambient space.
Example
“Let A and B be subspaces of a space S and suppose is an ambient homeomorphism taking A to B.” The point of this sentence is that A and B are not merely homeomorphic, but they are homeomorphic via an
automorphism of the space S.
and
between assertions
The word “and” between two assertions P and Q produces the conjunction of P and Q.
Example
The assertion “x is positive and x is less than 10” is true if both these statements are true: “x is positive”, “x is less than 10”.
between verb phrases
The word “and” can also be used between two verb phrases to assert both of them about the same subject.
Example
The assertion “ x is positive and less than 10” means the same thing as “x is positive and x is less than 10” .
between noun phrases
The word “and” may occur between two noun phrases as well. In that case the translation from English statement to logical assertion involves subtleties. This is an example of a translation problem.
Examples
¨ “I like red and white wine” means “I like red wine and I like white wine”. But so does “I like red or white wine!”
¨ “John and Mary go to school” means the same thing as “John goes to school and Mary goes to school”.
¨ “John and Mary own a car” (probably) does not mean “John owns a car and Mary owns a car”.
¨ Consider also the possible meanings of “John and Mary own cars”.
These examples show that the relationship between sentences containing the English word “and” and their logical equivalent is quite subtle. It is the main subject of Section 2.4 in
Kamp, H. and U. Reyle (1993), From Discourse to Logic, Parts I and II. Studies in Linguistics and Philosophy. Kluwer Academic Publishers.
Thanks to F. Schweiger for the wine example.
any
Used to
denote the universal
quantifier. Examples are discussed under that heading. See
also arbitrary.
arbitrary
Used to emphasize that there is no restriction on the mathematical structure referred to by the noun phrase that follows. You may usually use “any” in this situation instead of "arbitrary". In most cases the word adds no additional mathematical meaning to the statement.
Examples
¨
"The equation holds in an arbitrary group, but the
equation
requires commutativity."
¨ In a phrase such as "Let S be an arbitrary set" the word arbitrary typically signals an expectation of an upcoming proof by universal generalization.
Consciousness raising about arbitrary
People new to abstract math may have a systematic tendency
to underestimate how arbitrary a math object can
be. For example, the set is a perfectly good set. It is arbitrary, and, I admit, weird, but it
is a set. Other examples:
More arbitrary sets.
An arbitrary function.
Another arbitrary function.
argument
This
word has three common meanings in mathematical discourse.
¨ The angle a complex number makes with the real axis is called the argument of the number.
¨ The input to a function may be called the argument.
¨ A proof may be called an argument.
This word can cause cognitive dissonance. In English, “argument” can mean either:
¨ Organized step by step reasoning to support a claim, as in, “The judge’s argument for finding the suspect innocent was based on the fourteenth amendment.”
¨ The verbal expression of a disagreement, as in “George and Martha had an argument about the Venetian blinds.”
The meaning of disagreement is the common one and it may carry a connotation of unpleasantness. The three meanings in math that are given above have no connotation of unpleasantness.
assume To be written.
assumption
An assumption is an assertion that is taken as true in a given block of text that is its scope. "Taken as true" means that any proof in the scope of the assumption may use the assumption to justify a claim without further argument.
Examples
¨ "Throughout this chapter, G will denote an arbitrary Abelian group." In that chapter, a statement such as “The subgroup B of G is normal” can be taken to be true without further justification because every subgroup of an Abelian group is normal.
¨ A statement about a physical situation may be called an assumption. Such statements are then taken as true for the purposes of constructing a mathematical model.
¨ The hypothesis of a conditional assertion stands as an assumption during the statement of the assertion, and also through the proof if the proof is by modus ponens.
at least, at most
For real numbers x
and y, the phrase “x is at least y” means . The phrase " x is at most y" means
. When I say here that B
has at most one element, that means B
is either the empty set or a singleton
set.